Best Practices for Meshing Domains with Different Size Settings

Have you ever wondered about the best practices for structuring your meshing sequence? For instance, is there a difference between meshing domains in separate operation nodes and meshing them together using a single operation? In this blog post, we will discuss different ways of structuring your meshing sequence and how they affect the resulting mesh. You will gain insight into how the meshing operations behave when they are applied in a sequence.

An Introduction to Meshing Operations

There are two categories of meshing operations: structured and unstructured. The structured operations are Mapped and Swept, generating structured meshes, and the unstructured operations are Free Triangular, Free Quad, and Free Tetrahedral, generating unstructured meshes.

One significant characteristic of the unstructured operations is that they can mesh any geometry, whereas the structured operations require geometries that fulfill certain criteria. When an unstructured mesh is generated, both element quality and the specified size parameters are taken into account in order to achieve a mesh optimized for computations in the COMSOL Multiphysics® software. In addition to specifying size parameters, the way you structure your meshing sequence will also affect the resulting mesh. By studying a few examples, let’s sort out what these effects are and how you can use them to your advantage.

Choosing the Order of Your Meshing Sequence Operations

First, we will illustrate that the meshing sequence is order dependent. Let’s say that we have two neighboring squares in 2D that we would like to study. In the right square, we would like to have a finer mesh. This might be because the material demands it or because of the physics we plan to study.

We construct our meshing sequence by creating two Free Triangular nodes. In the first Free Triangular node, we select the left domain, and in the second node, we select the right domain (as shown in the image below). Next, we set the global Size node to the predefined value Extra coarse, because it’s recommended to specify the coarsest mesh size in the first global Size node.

Read further about using local and global Size nodes in the Using Meshing Sequences tutorial model (especially page 10 of the PDF documentation).

To specify the finer mesh size, we add a local Size node to the second Free Triangular node and specify the predefined size Extra fine.

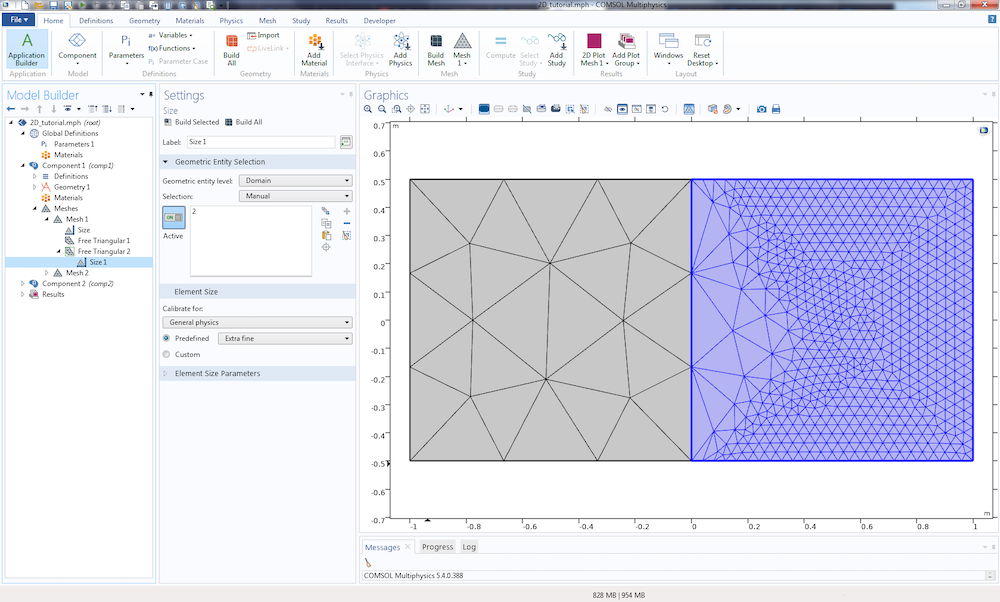
The meshing sequence contains a global Size node, two Free Triangular nodes, and one local Size node.

When plotting the resulting mesh, we can see that the left domain is meshed entirely by coarse mesh, while there are some coarse elements in the right domain near the shared boundary. This is because the boundary mesh of the shared boundary is fixed by the first operation, hence there cannot be any fine elements close to it. Moreover, the coarse elements on the right side of the shared boundary have a lower quality than the other elements.

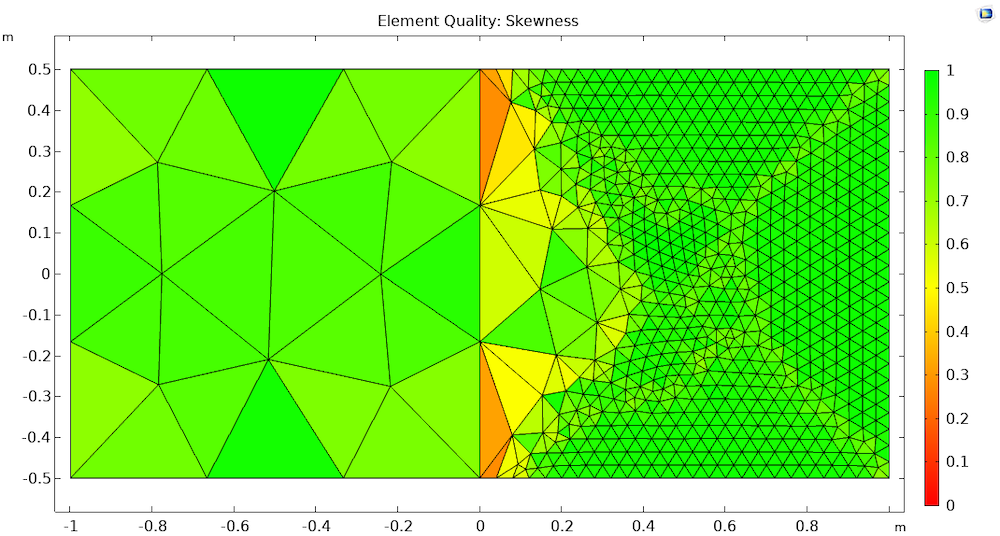
Resulting mesh when meshing the left domain first. There are some coarse elements of low quality in the right domain, even though we specified the mesh of the right domain to be Extra fine.

If we swap the order of the two Free Triangular nodes so that the operations are performed in reverse order (with the right domain meshed first), we get different results. In the resulting plot, we can see that the shared boundary now consists of finer mesh than before. As a result, the right domain now consists entirely of fine elements, while the left domain has some fine elements near the shared boundary. Consequently, the number of elements in the mesh has increased and the Minimum element quality has almost doubled, which means that the overall quality of the mesh has improved.

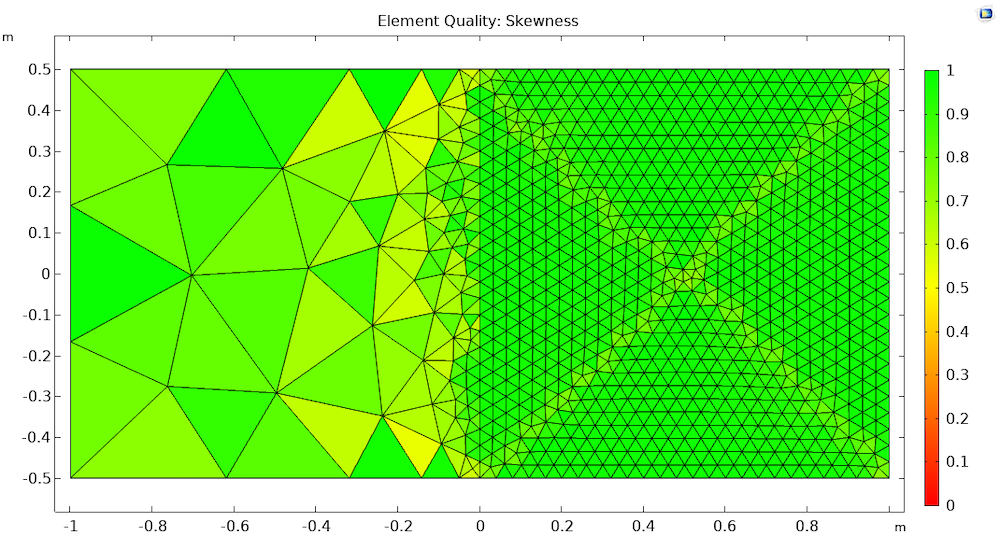
Resulting mesh when meshing the right domain first. The right domain now consists of only fine elements and the overall element quality is improved.

The takeaway here is that the mesh generated by an operation will act as a constraint on the mesh created by any following operation. In this example, this means that the mesh that is generated close to a previously meshed boundary will be affected by the element size of that boundary.

Using a Single Operation to Mesh Multiple Domains

Now, let’s consider a slightly different example. Say we have the same square setup, but each of the squares have a circular hole near the shared boundary. In this example, we will assume that we want both domains meshed with the same element size. Similar to the previous example, we construct our meshing sequence by adding two Free Triangular nodes to our meshing sequence and applying them to one domain each. This time, we set the global Size node to the predefined size Normal and we don’t add any additional Size nodes.

The plot of the resulting mesh does not look as satisfactory as we might have hoped. When studying the plot, we can see that the elements in the narrow region between the shared boundary and the lower hole have poor quality. Since the left domain is meshed first, the geometry of the right domain is not taken into account when generating the boundary mesh. Because the region between the lower hole and the boundary is narrow, it requires smaller elements than those generated on the shared boundary to avoid low-quality elements.

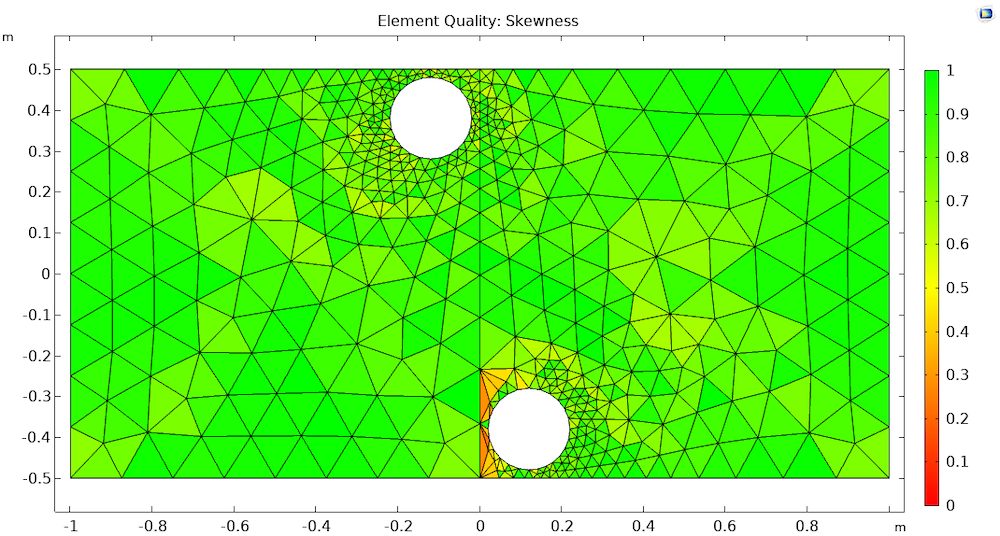
Resulting mesh when meshing the left domain first. The first operation, meshing the left domain, does not consider the geometry of the right domain. As a result, the narrow region between the shared boundary and the lower hole contains low-quality elements.

This sequence setup will not be able to generate a mesh that has high-quality elements in all regions of the geometry. Swapping the order of the operations will not help in this case, since the problem would just move to the upper narrow region instead. The solution here is to only use one Free Triangular operation and apply it to both domains, which allows the meshing algorithm to consider the entire geometry simultaneously and construct a boundary mesh suitable to both domains.

Read the previous blog post “Improved Capabilities for Meshing with Tetrahedral Elements” for a detailed description about the process for generating a tetrahedral mesh.

When we plot the mesh generated by a sequence with only one operation, we can see that the element quality has improved majorly in the lower narrow region.

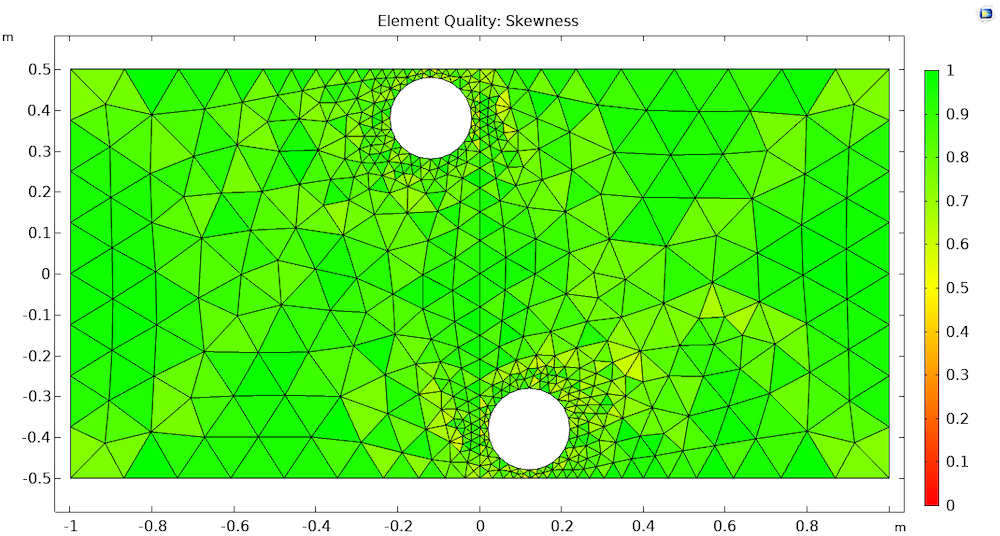
Resulting mesh when meshing both domains simultaneously. The mesh quality is improved in the lower narrow region, since the boundary mesh is generated in respect to both domains.

Even though we might have the same size specification in two adjacent domains, the order in which we mesh them can have a large impact on the resulting mesh. It’s important to note that when multiple domains are meshed in the same operation, the computer is able to generate the mesh in parallel. For these reasons, it’s recommended to use as few operations as possible.

A 3D Example

Finally, we will study a coil inside a box in 3D in order to see how these effects can appear in more advanced geometries. The coil we are using is the adaptable coil Single Conductor Coil – Rectangular Wire, Racetrack, Closed Side, available in the AC/DC Module Part Library. In our model, we add a box around the coil and adapt the coil so that the region between a pair of turns becomes very narrow, meaning a very fine mesh is required between the turns to avoid low quality elements. In this example, we would like to generate a mesh that is coarse in the surrounding box, a bit finer in the coil, and sufficiently fine in the narrow regions between the turns.

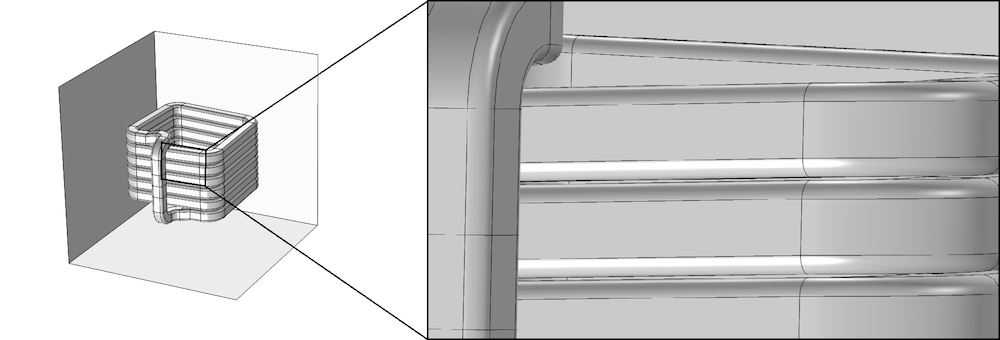
The coil geometry. The zoomed in view shows the narrow region between the coil turns.

We start constructing our meshing sequence by setting the global Size node to the predefined value Coarse. To obtain a mesh with sufficiently small elements in the narrow region, we have to adjust the parameter Minimum element size so that we can resolve the narrow region, which has a height of about 1.7e-4 m. This is done by selecting Custom in the global Size node and editing the Minimum element size to be 2e-4 m, as in the following image. Next, we add two Free Tetrahedral operations and select the coil in the first one and the surrounding box in the second. To the first Free Tetrahedral node, the one acting on the coil, we add a local Size node set to the predefined value Normal.

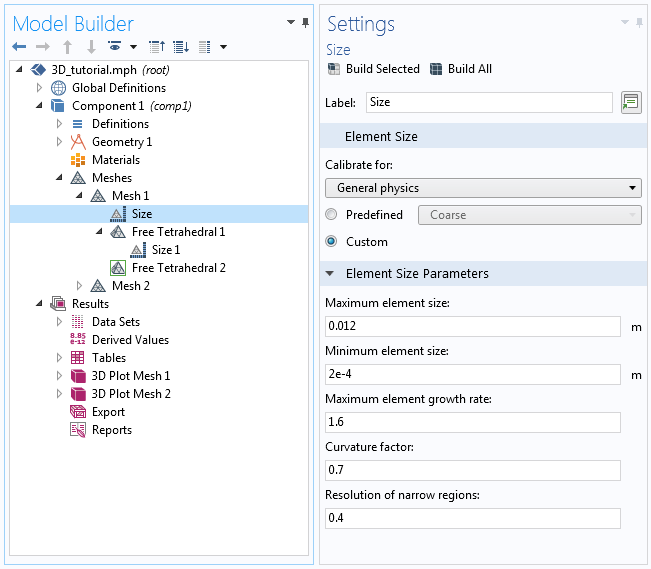
The global Size node is set to Coarse and then the Minimum element size is set to the custom value, 2e-4 m.

In the plot below, we can see results similar to those from the 2D examples: The narrow regions have elements of very poor quality, even though we specified a small Minimum element size. Again, this is a result of the ordering of the meshing operations. When the coil is meshed by the first operation, the narrow regions in the surrounding box do not act as a constraint on the element size on the boundary. Therefore, the boundary mesh is generated according to the specified mesh size on the coil, namely Normal. When the surrounding box is meshed, the mesh of the shared boundary is fixed, hence the mesh elements in the narrow regions are forced to have a skewed shape.

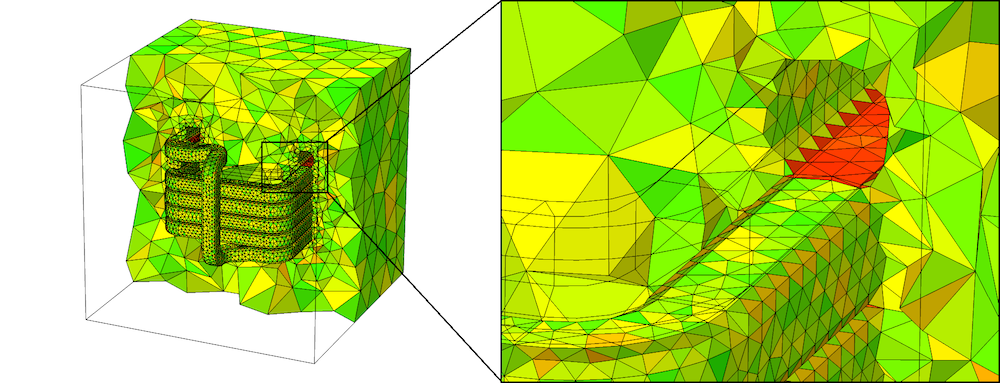
Resulting mesh when the coil is meshed first. Note that half of the box and one of the coil turns have been excluded for visibility. Since the coil is meshed first, the tetrahedrons generated in the narrow region (red) are of poor quality.

Next, we construct a new meshing sequence following our best practices. A single Free Tetrahedral operation is added and applied to the entire geometry. We add a local Size node to the operation with the default value Normal and the coil as the domain selection (as seen in the image below). The global Size node is set as in the previous sequence.

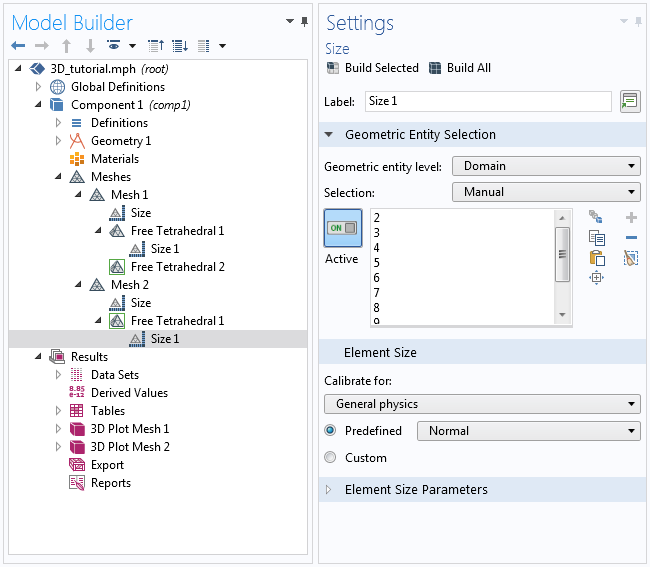
The local Size node specifies the element size for domains 2–11, which represent the coil.

When building this meshing sequence, the boundary mesh of the coil boundaries is meshed a lot finer to respect all of the surrounding geometry. As a result, the mesh elements generated in the narrow regions are finer and of better quality.

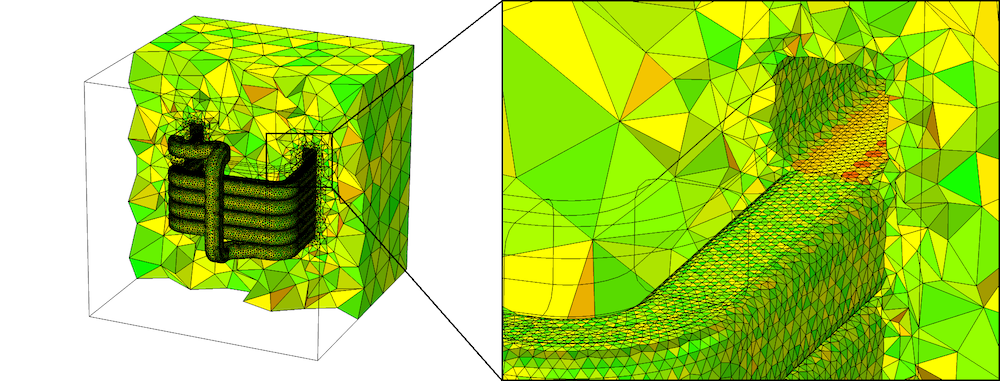
Resulting mesh when both domains are meshed simultaneously. Since the entire geometry is meshed in one operation, the mesh on the interior boundary is a lot finer than before, allowing the elements in the narrow region to have better quality.

Summary

In conclusion, we have seen that the order of operations in a meshing sequence has an effect on the resulting mesh. This is because the generated mesh is fixed, hence any mesh from a preceding operation node is a starting point for following operations. For this reason, it’s best practice to use as few operations as possible and either add Size nodes globally or locally. Additionally, if you need to have multiple operations in your sequence — for instance, if you want to have different element types — then it’s very important for you to consider their order.

Learn More

If you are interested in learning more about related topics, we recommend the following resources:

• Try the Free Tetrahedral Meshing of a Piston Geometry tutorial model
• Watch this video on building the mesh for a model geometry in COMSOL Multiphysics®