
Depending on their magnitude and frequency, vibrations can be a source of discomfort and even pain for the human body. The impact of these vibrations is surely felt, but wouldn’t it be interesting to visualize how different parts of the human body respond when placed in such an environment? We introduce you to a multibody model that enables you to analyze the body’s dynamic response to vibrations.
An Automotive Approach
Whether traveling a far distance between work and home or simply caught in a continuous wave of traffic, many of us spend a great deal of time on the road each day. On days where your evenings are free, this might be thought of as a time to relax and listen to a favorite CD or radio station. However, on days where your schedule is a bit more hectic, the lengthy commute can become a source of frustration as you race to make it on time to your destination. No matter the situation, an element that you rely on to make your car ride more enjoyable is comfort within your vehicle.
While on the road, you may have noticed the sensation of vibrations that can sometimes arise from your seat. The root of these vibrations can be traced to a number of sources, including road conditions, speed, engine vibrations, and the design of the vehicle’s seats. While not only a source of discomfort, prolonged exposure to such oscillations can be hazardous to one’s health, potentially resulting in fatigue or pain. With the growing concern behind the impact of these vibrations, some vehicles have begun to implement vibration isolators within the design of their seats in an effort to minimize this effect.

A vehicle’s seat can be a source of vibrations. (“Sedile in pelle di un’Alfa Romeo Giulietta” by Pava — Own work. Licensed under Creative Commons Attribution Share-Alike 3.0, via Wikimedia Commons).
With this biomechanical model built using the Multibody Dynamics Module, we can simulate the human body’s response to such vibrations, thereby helping to optimize the design of vibration isolators as well as analyze ride quality in vehicles.
Establishing Connections in the Biomechanical Model
The Biomechanical model of the human body in a sitting posture makes this analysis possible. An important element in the design of this model is addressing the complexity of the human body and how the different body parts are connected. In this example, we focus on the vibrational impact in six different areas of the body: the head, the torso, the viscera, the pelvis, the thighs, and the legs. Each element is treated as a lumped mass and defined as a rigid body.
To approximate the connections between varying body parts, we apply translational and rotational dampers and springs on the relative motion between the two connected body parts — a connection that is modeled with the elastic version of a fixed joint. This provides the translational and rotational stiffness and damping values between the connected body parts.
A fixed joint is used to model the connections between the body parts directly touching the seat (the legs, the thighs, and the pelvis) and the seat itself, which is the source of the vibration. To model the seat’s cushioning effect, elasticity on the joints is included when needed.
Note that rather than modeling the seat itself, a base motion node is used where the input excitation is 1 m/s2 in the vertical direction at three different locations.
Evaluating the Impact of Vibrations on the Human Body
We begin with an eigenfrequency analysis designed to determine the damped and undamped natural frequencies of vibration.
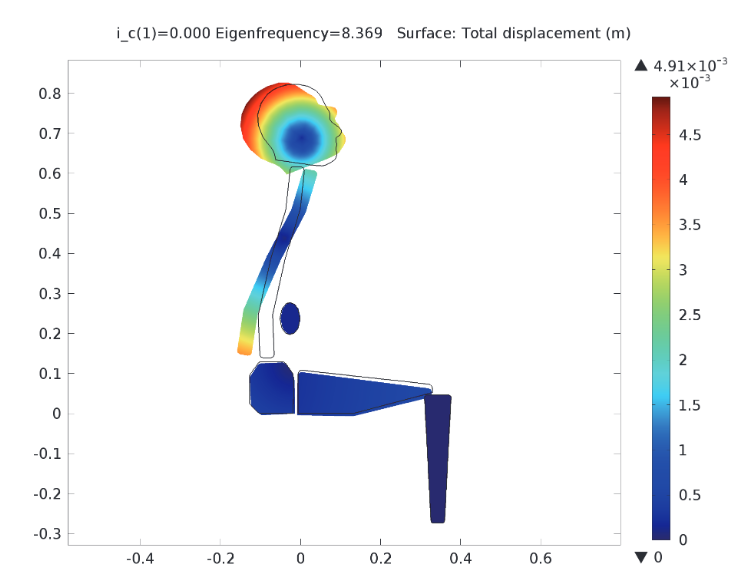
The figure below illustrates a rotational eigenmode on the undamped model. Considerable rotational movement is noted in the head and the torso. In comparison, little movement is found in other parts of the model.
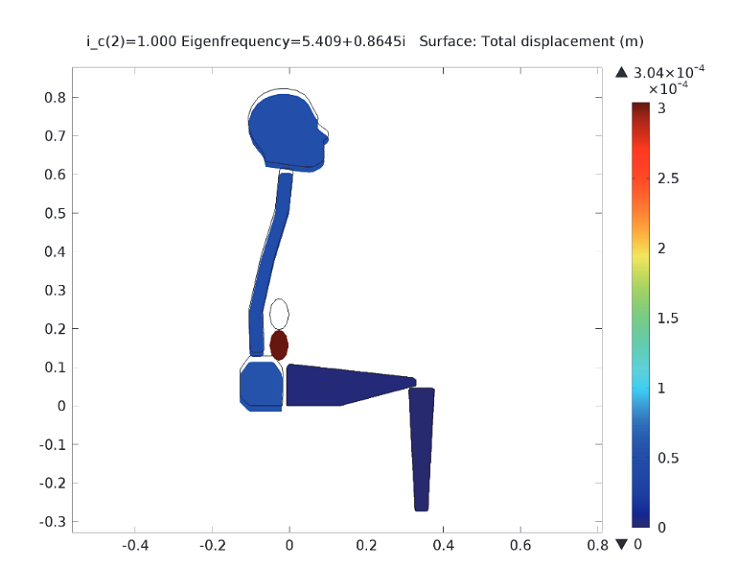
We then shift our analysis to the translational eigenmode of the damped model. In the first major translational eigenmode, the results indicate a downward movement in the head, the pelvis, and the viscera, with no significant movement noted in the other body parts. This is illustrated in the figure below.
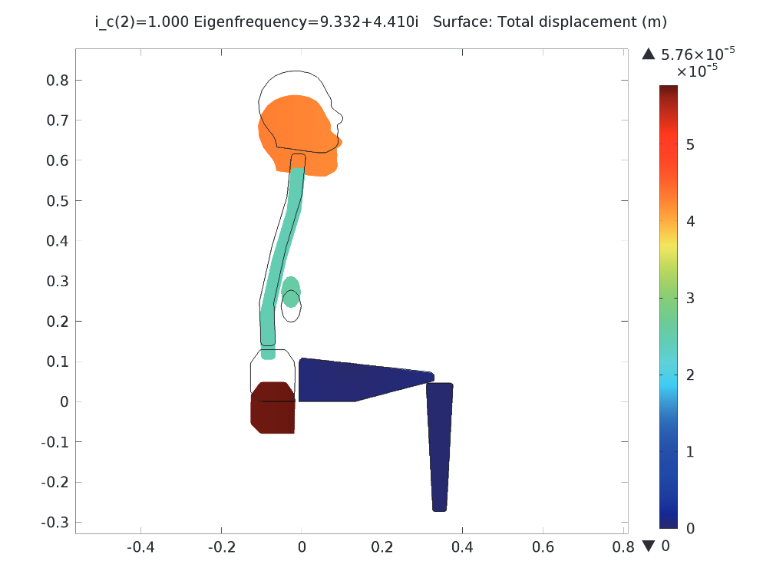
The second major translational eigenmode (shown below) notes displacement in the downward direction of the head, the torso, and the pelvis, whereas the viscera moves in the upward direction.
Frequency Response Analysis
This example then features a frequency response analysis around the natural frequencies to analyze three different elements: vertical transmissibility, rotational transmissibility, and apparent mass.
Let’s first focus our attention on vertical transmissibility. Vertical transmissibility refers to the ratio between the head’s vertical acceleration and the seat’s input acceleration. When compared with the excitation frequency, the results show that the primary resonance is visible in the range of 4-6 Hz and the secondary resonance in the range of 8-10 Hz.
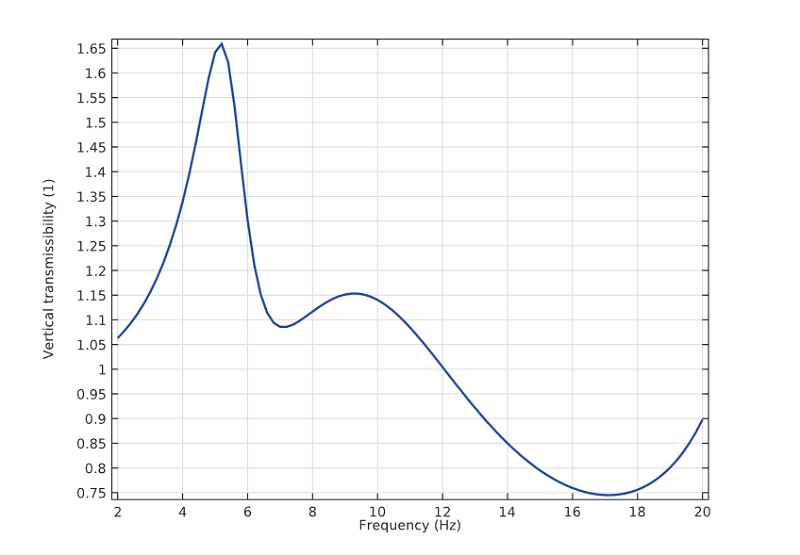
Vertical transmissibility vs. excitation frequency.
Rotational transmissibility is the ratio between the head’s angular acceleration and the seat’s input acceleration. With regards to this form of transmissibility, it is important to avoid high values as this can enhance discomfort as well as affect one’s vision. The plot below depicts its variation with the excitation frequency.
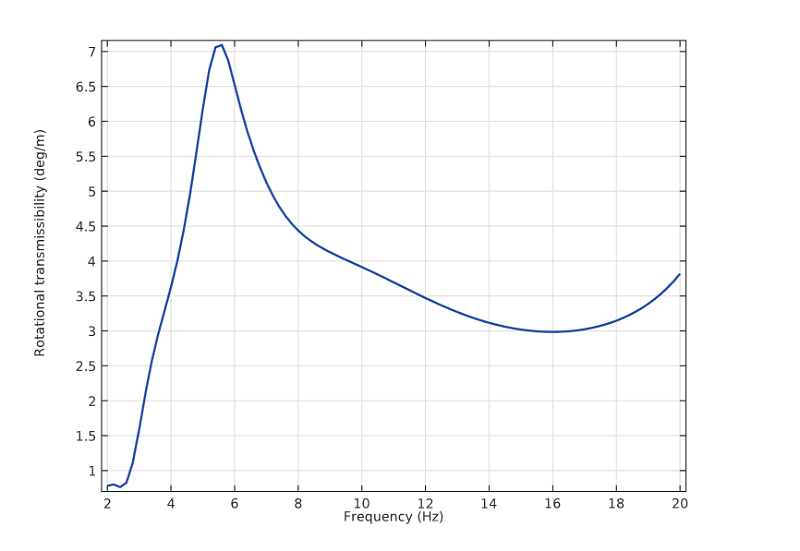
Rotational transmissibility vs. excitation frequency.
Finally, apparent mass refers to the ratio of the seat’s force to the seat’s input acceleration. Rather than depicting the end point characteristics of the model, this element conveys the driving point characteristics.
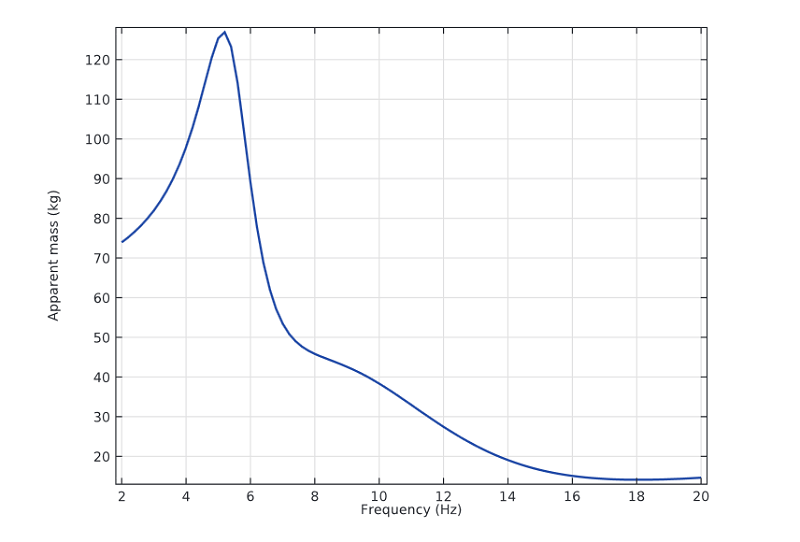
Apparent mass vs. excitation frequency.
Concluding Thoughts
In this blog post, we have introduced you to a biomechanical model of the human body, particularly highlighting its application within the automotive industry. We have showed you how, with the Multibody Dynamics interface, you can model various parts of the human body — and their connections — as well as analyze its dynamic response to whole body vibrations.




Comments (0)