
When designing magnets, you want to save resources by using as little material as possible, while generating as large of a force as possible on the object in question. To calculate the force of a one-sided magnet, you can use COMSOL Multiphysics and the AC/DC Module.
One-Sided Permanent Magnets
Chances are, you have some magnets on your refrigerator at home or on the whiteboard in your office. This is one common use of one-sided permanent magnets, but they are also used in more advanced applications, such as particle accelerators, magnetic resonance imaging (MRI) machines, and magnetic levitation (maglev) in high speed trains, to name a few.
As you may know, a conventional magnet has north and south poles. Its magnetic field emanates from its north pole and curves back into the opposing south pole, making it a magnetic dipole. One-sided magnets, on the other hand, appear to have a single pole on one side, as illustrated below.
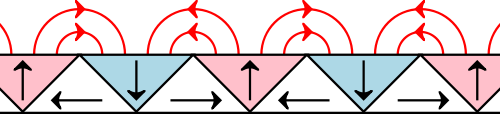
The flux distribution of a refrigerator magnet.
Obtaining One-Sided Flux Behavior
To model a one-sided magnet, you can follow the instructions in our One-Sided Magnet and Plate example model, which uses a mathematical expression incorporating data from the “One-sided fluxes in planar, cylindrical, and spherical magnetized structures” paper from IEEE. Alternatively, you can model the one-sided flux behavior by arranging the magnets in such a way that the net magnetic field is augmented on one side and cancelled on the other side, as shown in the section below.
Magnetic Shielding
To calculate the accurate force, you will need to model the object the magnet is sitting next to. But, modeling the entire whiteboard, fridge, or what have you, in 3D would be computationally expensive. Therefore, instead you can take advantage of a magnetic shielding boundary condition in the AC/DC Module.

Magnetic flux density arrow plots of one-sided permanent magnets. One plot with a magnetic material model (left) and another with a magnetic shielding boundary (right).
Modeling the magnetic shield as a plate instead of the whole 3D object saves time. A common material used for this purpose is \mu-metal, a highly permeable and ductile metal alloy. You can assign different material properties to the plate to see how it affects the results.
For instance, some applications require you to take magnetic saturation effects into account. To do so, you can model the plate using nonlinear magnetic material. Instructions for this can also be found in the model documentation.
Calculating the Magnetic Flux
If you set up and solve this model using the AC/DC Module, you will see that the force generated by the one-sided magnet is substantial.
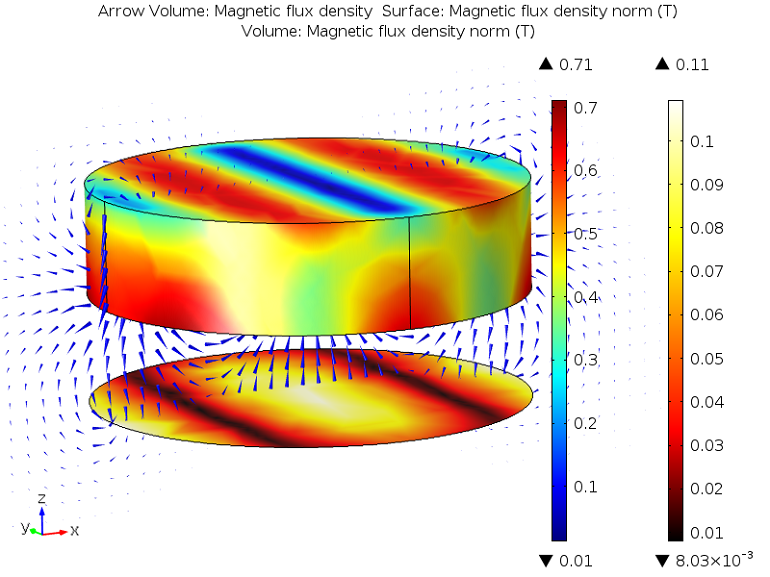
The magnetic flux density on the magnet and the magnetic flux density direction is plotted in a cross section of the geometry. The magnetic flux density in the plate is shown on the separate scale.







Comments (0)