CFD Applied to Two-Phase Flow, an Italian Dressing Simulation

The fact that oil and water don’t mix is something that you are probably all familiar with. At one point or another, you’ve most likely noticed what happens when you shake a bottle of say, Italian salad dressing, and the liquids mix momentarily, only to become separated again within seconds as oil bubbles rise to the surface. Creating a simulation describing how these two immiscible fluids interact is a great way to introduce computational fluid dynamics (CFD) applied to two-phase flow.

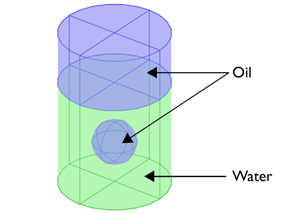
Figure 1: Mixture of two immiscible liquids — oil
and water — showing the initial position of an oil
bubble trapped in water.

What are immiscible liquids?

Before we get into the simulation, let’s make sure we understand some of the physics at hand. First of all, what are immiscible liquids? Immiscible liquids are two or more liquids that are incapable of mixing together. This occurs because the molecules that make up the liquids are characterized by different types of chemical bonding. In the case of oil and water, water is a polar molecule, while oil is a nonpolar molecule, and therefore the two substances are unable to mix. Pouring the liquids together will result in two distinct phases separated by a clearly defined interface.

Miscible liquids, on the other hand, will mix together to form a single liquid phase with no interface visible between them. This occurs between liquids of a similar polarity.

To continue to use Italian salad dressing as our example, we have a combination of two types of liquids: immiscible and miscible. Typical Italian dressing contains vinegar, water, lemon juice, and oil. The first three ingredients have polar molecules, and are therefore miscible. Since oil is nonpolar, the polar ingredients mix together, resulting in a mixture that is immiscible with oil — the contents of our dressing bottle involve two-phase flow. If we give it enough time, and simulation can compute it, the lighter phase (oil in our case) will rise to the top, while the more dense phase will settle at the bottom. This is why we should always shake the dressing bottle before pouring it on our salad (we don’t want a single-phase, oily Italian dressing!).

Modeling Two-phase Flow using CFD

Using COMSOL Multiphysics in combination with the CFD Module, we can set up a simulation describing two immiscible liquids — oil and water for example — and then measure how the separating interface changes its shape in time as buoyancy effects cause an oil bubble to rise through the water. You can set up and solve this model by following the step-by-step instructions that accompany the Rising Bubble model available in the Model Gallery.

At the beginning of the simulation, there are three different domains that need to be represented: the oil phase, the water phase, and the oil bubble immersed in the water phase (see figure 2). In our simulation, the oil phase has a viscosity of 0.0208 Pa·s and a density of 879 kg/m³, and the water phase a viscosity of 1.01·10⁻³ Pa·s and a density of 1,000 kg/m³. With the CFD Module, we can choose to use the level set method or the phase field method to model topology changes due to the interface motion as the bubble rises through the water phase and then merges with the oil phase again. When we set up the model and choose the level set method, two study steps are automatically created; one initializes the level set function, and the second solves Navier-Stokes equations for a two-phase flow problem where mass transport, momentum transport, surface tension forces, and interface motion are taken into account.

At the beginning of the simulation, the bubble’s shape remains spherical as it rises, due to the surface tension of the bubble and oil’s high viscosity. The bubble’s trajectory as it moves through the water can be seen in the images below, where blue is the water phase and red is the oil phase. Because the problem is axisymmetric, we can simulate it by using an axisymmetric geometry to save on computation time, while still generating accurate results.

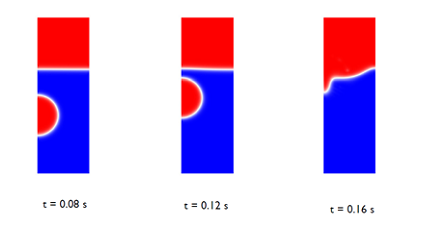
Figure 2: Snapshots showing the interface prior to and just after the
bubble hits the surface.

As the bubble reaches the surface of the water phase, it merges with the oil, creating waves on the surface of the water phase. The waves can be seen in the images below:

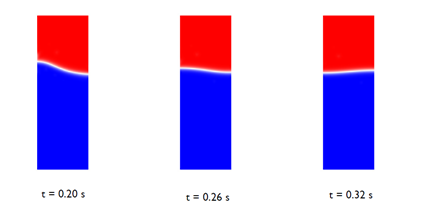
Figure 3: Snapshots showing the interface after the bubble has merged
with the oil above.

One way to check if the numerical results are accurate is to examine the conservation of mass in the model. Since there is no flow through boundaries, the total mass of both the oil and water should be constant throughout the simulation. This can be easily calculated using COMSOL Multiphysics capabilities to determine the change in total mass over time. For this simulation, the results are shown in the graph below.

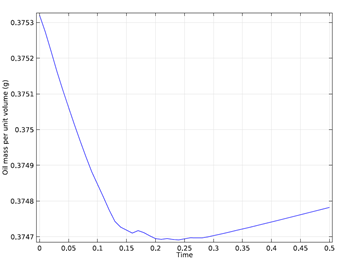
Figure 4: Total mass of oil as a function of time. The total mass
loss during the simulation is less than 0.2%.

As you can see in the graph, the total mass lost during the simulation is less than 0.2%, which suggests that the accuracy of the numerical results is good.

Download the Model

• Rising Bubble model