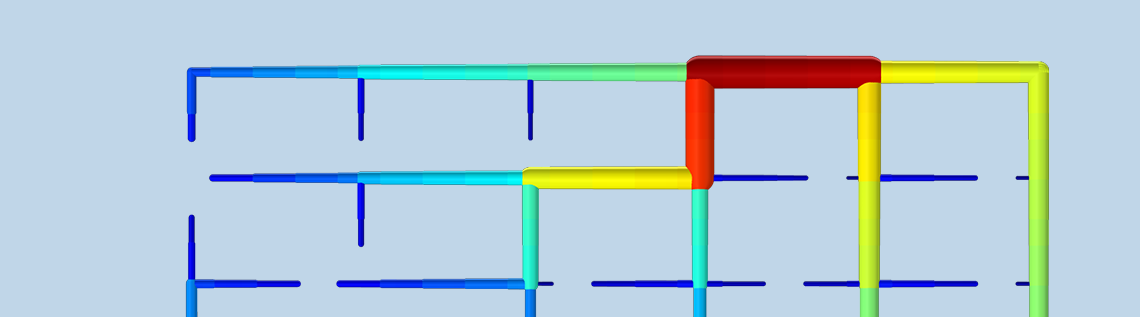
In the winter, power plants can reach high efficiencies by utilizing cogeneration. How? By relying on district heating networks. The design of such networks has previously been limited to inaccurate linear models or nonlinear models of small networks. Recent research has demonstrated that gradient-based optimization can be used to design large networks using nonlinear models (Ref. 2). In this blog post, we will reproduce this research using the COMSOL Multiphysics® software as well as the Pipe Flow and Optimization modules.
What Are District Heating Networks?
Power plants for electricity generation often convert less than half the input energy to electrical energy. It is possible to increase the efficiency by capturing the heat generated in the process. The heat can be used for residential heating in urban environments.
To make this heating system a reality, you have to construct a network of pipes for distributing the heat. The technology can allow efficiencies of up to 80% in the winter time (Ref. 1)!

An example of a district heating pipeline from Tübingen, Germany. Image by Björn Appel — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
Modeling a District Heating Network
The model discussed in this blog post considers identical consumers, continuous pipe diameters, and a simple model for the radiators and network heat loss. This means that the resulting network topology is likely to be good, but in order to trust the quantitative values for the pipe diameters, it might be necessary to use more advanced expressions and techniques, as done in Ref. 2.
Topology Optimization
The optimization problem consists of controls, constraints, and objectives. Let’s go over what each of these factors mean in relation to the optimization problem.
Controls
District heating networks are generally aligned with road infrastructure, so the question of how the network should be designed can be reduced to the following questions:
- Which roads should have pipes?
- How large should these pipes be?
Consumers are generally charged fees for returning heated water too hot, because this constitutes a waste of pumping energy. Consumers thus have an incentive to decrease the flow speed over the heat exchanger that connects the heating network to the heating system of their property. However, this can lead to low flow rates in the system, which can cause low temperatures for consumers far from the producer due to heat lost from the network to the ground. To prevent this issue, the heating network is equipped with bypass valves in the end of the network so that an adequate flow rate can be ensured.
Because we do not know the end points of the network, we simply treat each producer as a bypass valve and optimize the diameter of this valve. We also optimize the radiator controls for the individual users, which effectively determines the coupling constant between the room temperature at the consumer level and the heating fluid of the network. Finally, we allow the driving pressure over the network to be optimized.
Constraints
In order for the network to be valid, it has to be able to distribute sufficient heat, P, to all consumers, but a large network will have many consumers leading to many constraints, which can be numerically problematic. A popular solution to this problem is to use a constraint aggregation technique, so that a large number of linear constraints is converted to a single nonlinear constraint, i.e.,
The violation of local constraints will decrease with larger values of \beta, but the large values will also cause numerical problems. Therefore, in practice, a compromise has to be found.
Objectives
The primary cost of establishing the network is related to the total length of trenches that have to be dug, but larger pipes also cost more than smaller pipes, so we can approximate the cost as
where D is the pipe diameter, b is the cost of digging a trench, and a is a parameter that accounts for the fact that bigger pipes are more expensive to buy and install. The values of a and b are estimated based on Ref. 1.
By itself, this would lead to a network with very small pipes and a large pressure drop, requiring an expensive pump. This can be avoided by adding a term related to the pumping power, so that the total objective function becomes
The constant relating the pumping power to the objective function depends on several things, such as the maintenance cost of the network, the price of electricity, and the cost of capital.
Results of the District Heating Network Optimization Problem
Each consumer requires 5 kW of heating power. The consumers are arranged in rectangles corresponding to city blocks, which in turn are repeated in an array. The network has a heat producer delivering 70°C in the southwestern corner and another heat producer delivering 65°C water in the north.
The model starts out by optimizing the bypass and radiator controls, with the constraint, C, as the objective function. The result of this is used as an initial guess, when minimizing \mathrm{EUR}_\mathrm{total}.
The first plot shows the optimized pipe diameters together with the heating power for each consumer. The network design branches into smaller and smaller pipes, as one would expect. In this case, we consider a situation where there are consumers almost everywhere, and this makes it difficult to reduce \mathrm{EUR}_\mathrm{Pipe}.
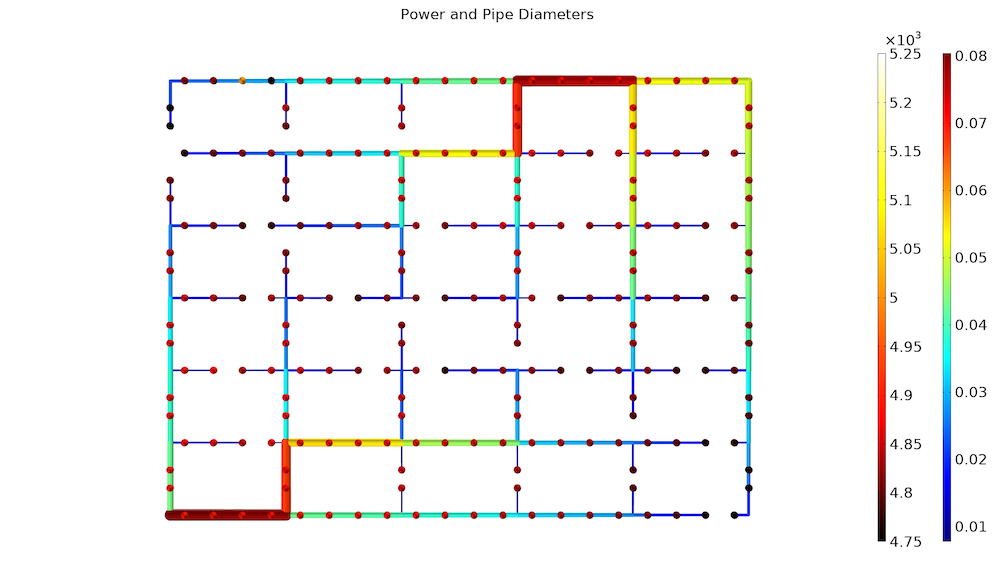
The network topology is shown with the consumer heating powers. The minimum power is 4.7 kW, so none of the consumers are freezing.
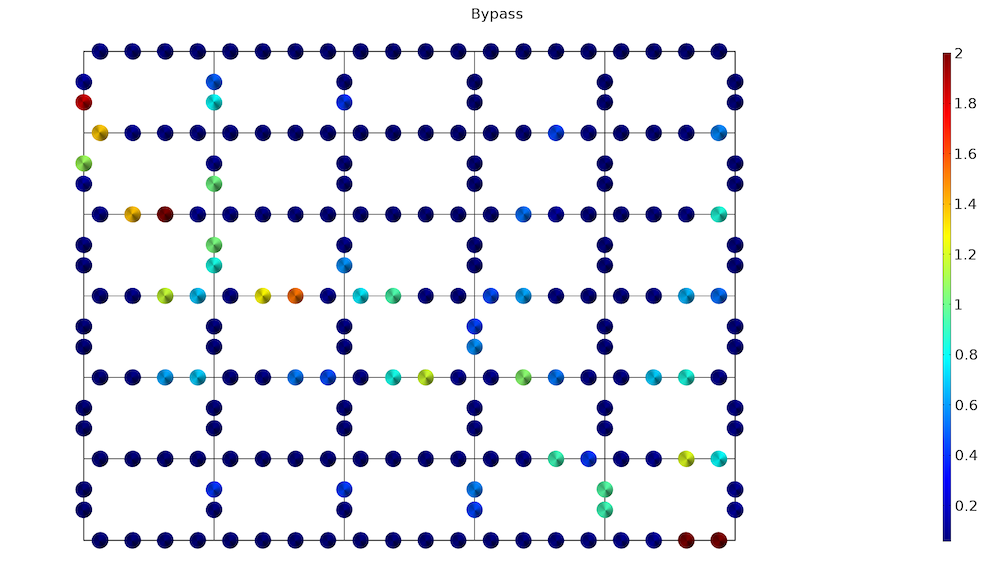
The second plot shows the values of the bypass controls. As expected, the valves are mostly closed, except in the very end of the two networks.
Finally, we can look at the consumer radiator controls and conclude that the consumers belonging to the network with a 65°C inlet temperature need to turn their radiators up a bit more than the consumers belonging to the hotter network. The optimization is performed with a rather large maximum value for the radiator controls, so the maximum bound never becomes active. The bound value can be lowered to allow for radiators with mediocre performance, but the overall economic cost might be lower by going for better radiators in the very end of the network. One could answer this question by including the cost of radiators in the objective function.
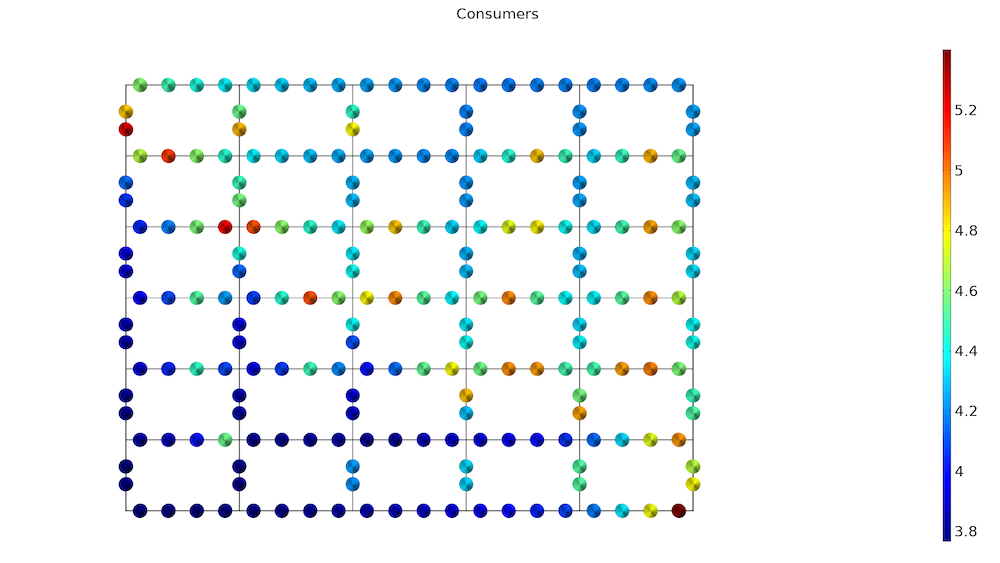
The consumer radiator controls.
Next Steps
You can extend the model with the techniques used in Ref. 2, write a model method supporting the import of a road network from OpenStreetMap, and create a simulation app for designing distributed heating networks. The app can return a shopping list for the pipes and estimate the cost for the consumers, so that the feasibility of establishing a network can be evaluated.
References
- “How Gas Turbine Power Plants Work”, Office of Fossil Energy, https://www.energy.gov/fe/how-gas-turbine-power-plants-work.
- M. Blommaert, Y. Wack, and M. Baelmans, “An adjoint optimization approach for the topological design of large-scale district heating networks based on nonlinear models”, Applied Energy, vol. 280, 2020.




Comments (0)