Estimating Parameters for a Li-Ion Battery via a Lumped Model

Lithium is used in all sorts of settings, but batteries are perhaps the most notable. Lithium-ion batteries are helpful for electric vehicles, energy storage systems, and more; however, engineers must first make sure they will perform as expected via electrochemical analysis. This can pose as a problem when batteries are manufactured by a third party: Information about key factors (like the internal structure) might not be shared with the battery engineer. Let’s see how a black-box simulation approach can help.

Editor’s note: At the time when this blog post was written, the Optimization Module was needed to solve the model. As of COMSOL Multiphysics version 6.1, only the Battery Design Module is needed.

Advantages and Design Challenges of Li-Ion Batteries

Lithium is the third element of the periodic table and has many extraordinary properties. It can act as a mood stabilizer when combined with carbonate and is an effective treatment method for bipolar disorder. When heated, it produces a red color that helps to color fireworks. It is the lightest metal on the periodic table, which is an extremely helpful quality when weight reduction is important, such as space travel and aircraft design. Lithium is also a good choice for batteries: In addition to being light, it has a high electrochemical potential and large energy density.

First proposed in the 1970s and developed in the 1990s, Li-ion batteries are one of the most popular types of rechargeable batteries and can be found in:

• Mobile devices, such as phones and tablets
• Solar energy storage systems
• Electric vehicles

Lithium-ion batteries are commonly used for mobile phones.

Before Li-ion batteries can be placed in cellphones and other devices, they must undergo some characterization, both for electrical and for thermal design purposes. This can be difficult, though, since batteries are often sourced from external manufacturing companies that may not provide details on the battery’s internal structure, like the thickness of the electrodes, particle size, and the specific chemistry of the electrode materials. Battery engineers need to know this information to analyze and design battery packs and thermal management systems. The data that may be of interest includes the open-circuit voltage as a function of state-of-charge (SOC); transport properties (e.g., diffusivity and conductivity); and potential losses due to different kinds of overpotential, including activation, concentration, and ohmic overpotential.

In order to design a battery system for a device, engineers can use lumped models, which may give reliable predictions within a given range of operation by performing parameter estimations via the COMSOL Multiphysics® software and add-on Optimization Module. Using this black-box approach, they can efficiently gain the information needed for predicting the electrical performance when the battery system is incorporated in a device and for running detailed thermal analysis — even with a few lumped parameters.

Creating a Lumped Li-Ion Battery Model

The Parameter Estimation of a Time-Dependent Lumped Battery Model consists of two parts:

1. Setting up and solving a lumped model of a battery
2. Performing a parameter estimation study

The transport and reaction processes in the electrodes may be described with one lumped diffusion-reaction equation. This is a so-called “single-particle” model, which greatly reduces computational resources compared to a more detailed model. Other losses like activation and ohmic losses are added on top. With the Lumped Battery interface, you can easily calculate how the battery cell voltage changes based on measured charge-discharge cycles. The lumped model describes how mass transport, charge transfer, and ohmic processes affect the potential loss for a battery using only a few lumped parameters.

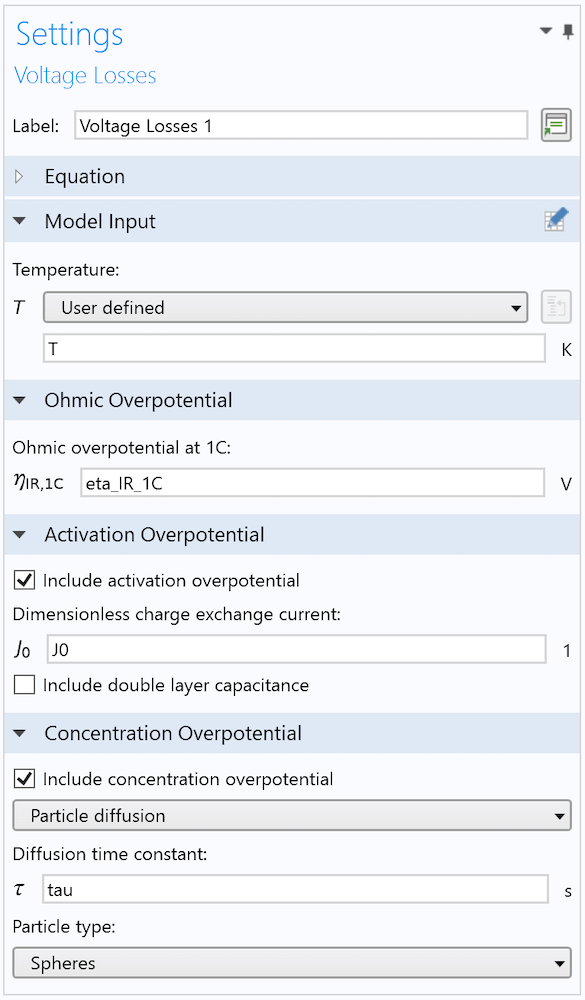
Only a few parameters are required in order to describe the lumped losses for a battery for use in, for example, thermal analysis.

For this example, you can input experimental data in order to define the battery capacity, the open-circuit voltage vs. SOC function, and the battery load. There are also parameters that are used in the parameter estimation study, including the ohmic overpotential at 1C, dimensionless charge exchange current, and diffusion time constant.

Next up is the parameter estimation study, which requires the Optimization Module — an add-on product containing dedicated features for improving various engineering designs. Here, you use the Optimization interface to specify a Global Least-Squares Objective function (which estimates the difference between measurements and model results and should therefore be minimized by finding the optimal parameter values in the study), and a Levenberg–Marquardt optimization solver and the Optimization node to specify which parameters need to be optimized.

As mentioned earlier, using this modeling approach will allow you to estimate unknown parameter values for the battery in less time than it would take for a more detailed model — and with less computational resources — while still obtaining a model that may be used for predicting performance and temperature of a battery pack design. Let’s take a look at the results.

Examining the Results of the Parameter Estimation

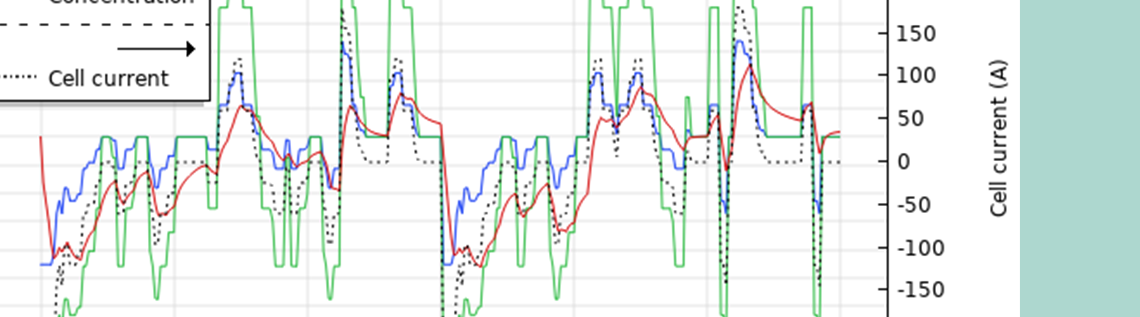
From the results, you can visualize the cell voltage and the current, which yield how much electric energy the battery generates. As the image below portrays, the model agrees well with the experimental data over time (five minutes). In addition, you can determine the maximum voltage available for the cell when there is no applied current, the open-circuit potential (OCP).

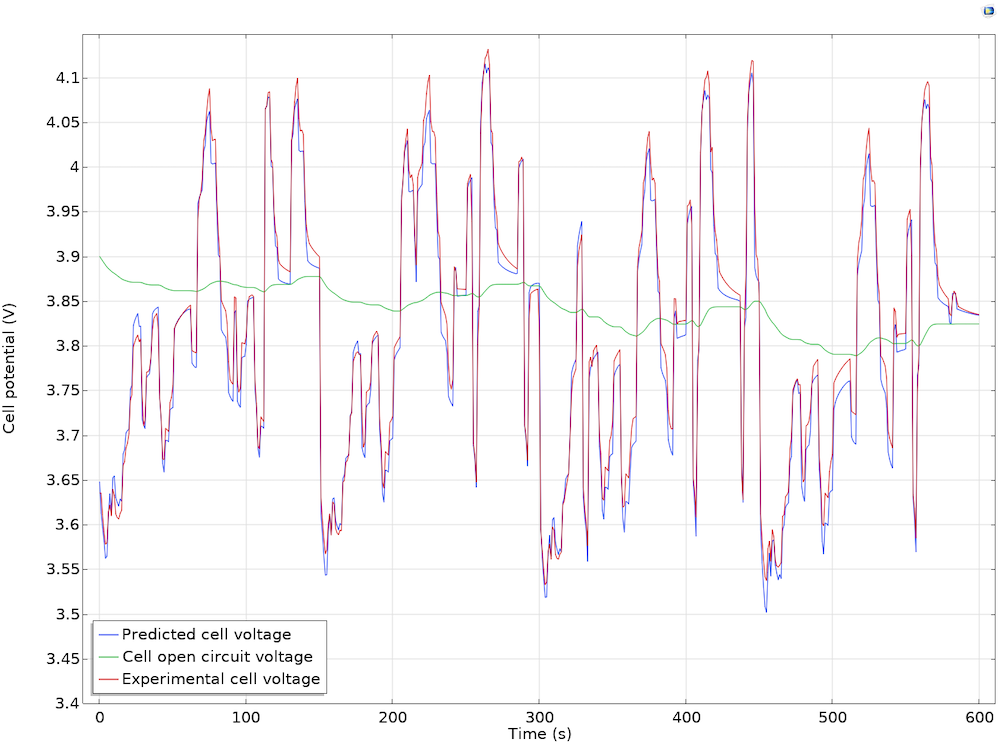
Modeled and experimental cell voltage for this battery example as well as the corresponding OCP.

The model can also help you analyze the effect of overpotential contributions and thus the battery’s efficiency. Typically, minimizing overpotential contributions can be difficult, as numerous nonlinear and time-varying aspects come into play. Using a lumped model, you can use the fitted parameters from the parameter estimation study to determine how overpotential (including activation, ohmic, and concentration) affects a design over time and for a varying cell current.

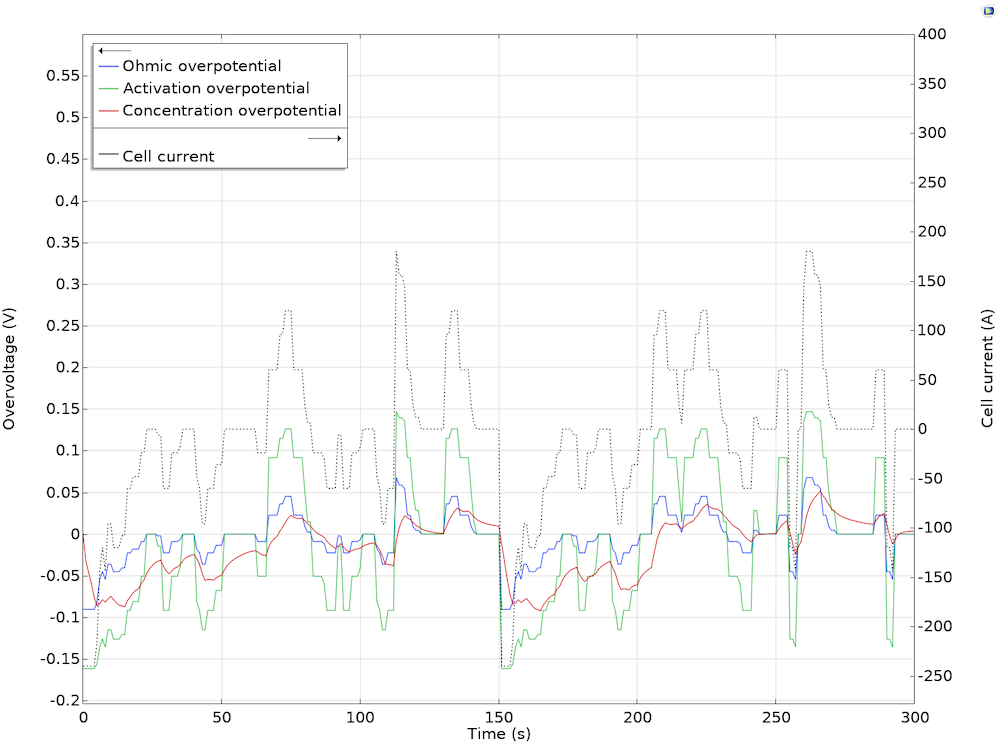
Losses from ohmic, charge transfer, and diffusional processes throughout a 5-minute time period and varying cell current.

Using this black-box simulation approach, you can obtain necessary information about a battery that can be used for battery pack design and design of thermal management systems for a battery pack.

Next Steps

Click the button below to try the Parameter Estimation of a Time-Dependent Lumped Battery Model from the Application Gallery. There, you can find the documentation and download the related MPH-file.

Further Reading

• Find out more about modeling lithium-ion models:
  • Evaluating the Electrode Utilization of a Lithium-Ion Battery Pouch Cell
• How to Model Short Circuits in Lithium-Ion Batteries
• Get more details on performing a parameter estimation study on the COMSOL blog:
  • How to Use the Parameter Estimation Study Step for Inverse Modeling
  • Multiparameter Optimization with a Least-Squares Objective