
Something that King Louis XVI and Napoleon most likely agreed on: Joseph-Louis Lagrange was a phenomenal mathematician. Lagrange won numerous awards throughout his prolific and varied career. He was part of King Frederick the Great’s court in Berlin and later accepted King Louis XVI’s invitation to move to Paris, where he lived for the rest of his life — including throughout the French Revolution. When Napoleon came into power, he gave Lagrange honors. Although Lagrange died in 1813, his legacy and achievements live on.
Early Life of Joseph-Louis Lagrange
Joseph-Louis Lagrange was born on January 25, 1736, in what is now Italy. His family was well-to-do, and his father was the treasurer to the King of Sardinia. Unfortunately, his father lost his wealth on speculation when Lagrange was young.
Unlike other famous mathematicians, Lagrange wasn’t consumed by math at an early age and had set out to the University of Turin to become a lawyer. But at 17, only a year after starting at the university, Lagrange discovered a paper written by Edmond Halley. Greatly inspired, he threw himself into math, and after just one year of study, Lagrange published his first mathematical paper. Just one year after that, at 19, he was a mathematics professor at the university. Thus began Lagrange’s prolific and groundbreaking career as a mathematician.

A portrait of Lagrange. Image in the public domain, via Wikimedia Commons.
Mathematical Career
Joseph-Louis Lagrange amassed a collection of awards from the French Academy of Sciences. His first was in 1764. He won another in 1772. And another in 1774. And yet another in 1778.
In 1766, two years after Lagrange’s first award from the French Academy of Sciences, Leonhard Euler retired from his position in King Frederick the Great’s court. King Frederick felt it was fitting that the greatest king in Europe (himself) have the greatest mathematician in Europe in his court. Euler recommended Lagrange, who accepted the position and moved to Berlin. Lagrange stayed in Berlin for twenty years and worked on a number of problems in various fields, including mechanics, probability, and fluid dynamics.
After King Frederick’s death, Lagrange received invitations from a number of royalty to join their courts. Ultimately, Lagrange accepted King Louis XVI’s invitation and went to Paris. It was here where published his magnum opus, Mécanique analytique. This treatise was groundbreaking: It synthesized the physics-related work of people like Euler and Bernoulli and transitioned physics from geometric to analytical methods.
Lagrange was not one for politics, which protected him during the French Revolution. Although he was prepared to flee France, he ultimately stayed and became one of the leading mathematics professors at École Polytechnique when it opened in 1794. Lagrange was also heavily involved in creating standards for the metric system at this time. Napoleon came into power in 1799. During his reign, he named Lagrange a senator and a count. Lagrange died at 77 in Paris on April 10, 1813.
The Legacy of Lagrange
Lagrange’s contributions to mathematics can be found in a wide variety of fields, so let’s just mention a few here. Some of these topics carry Lagrange’s name, although other people were also involved in their development.
Calculus of Variations
Lagrange, building on earlier work by Euler, developed the foundation of the mathematical field nowadays called calculus of variations. Conventional calculus, invented by Newton and Leibniz, deals with functions in terms of coordinate variables, such as x, y, and z, and conceptual infinitesimal quantities, such as dx, dy, and dz.
Calculus of variations is a generalization of this concept and is the analysis of “functions of functions”, called functionals, where the infinitesimal quantities are called variations. The variation of a function f is usually written as \delta f. Similar to the way traditional calculus can be used to find the coordinate that will minimize a function, calculus of variations can be used to find a function, among a set of functions, that minimizes a type of energy-like quantity, the Lagrangian. This minimization procedure results in Lagrange’s equation as well as the Euler–Lagrange equations.
The theory of calculus of variations allowed for a reformulation of Newtonian mechanics in terms of the Lagrangian, so-called Lagrangian mechanics. Over the years, this has been generalized in different directions with applications in quantum theory, finite element theory, and optimization theory.
The Theory of Lagrange Multipliers
Another one of Lagrange’s contributions is the method of Lagrange multipliers, a general strategy for optimization with equality constraints. This method has numerous applications in linear and nonlinear optimization, mathematical physics, optimal control, finance, etc.
Lagrangian multipliers can be used to enforce constraints in variational problems, like a catenary, as well as in optimization methods, for finding the local maxima and minima of a function subject to equality constraints.
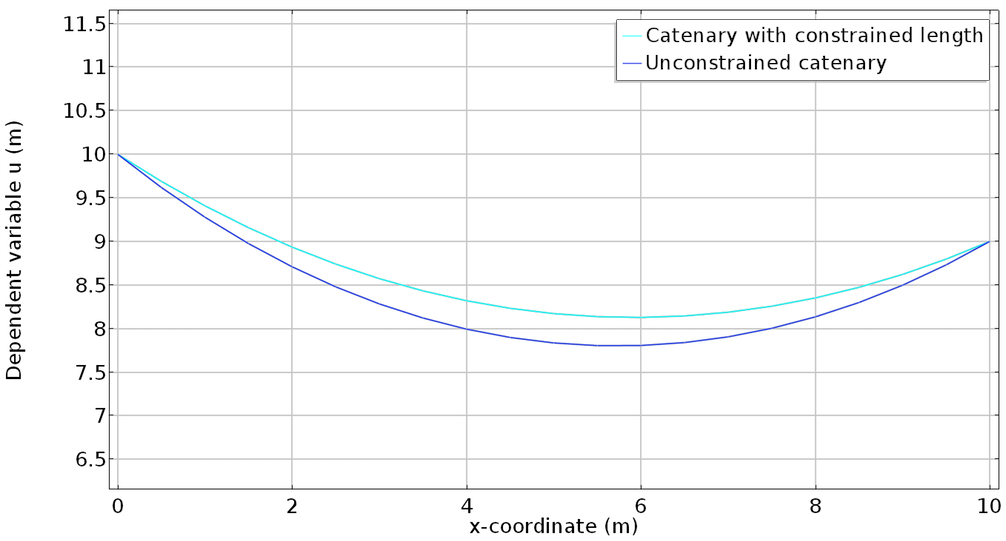
A constraint problem of a catenary, which uses Lagrange multipliers.
Deforming Geometries
The arbitrary Lagrangian–Eulerian method, which combines the work of Lagrange and Euler, is used to model deforming geometries and is integral to analyzing fluid-structure interaction (FSI) problems.
A FSI simulation of fluid flow through a micropump. The deformed mesh is found via the arbitrary Lagrangian–Eulerian method.
Lagrange Polynomials
Lagrange finite elements, or shape functions, use Lagrange polynomials, from theory of interpolation, and are one of the most common of the underlying fundamental elements in the finite element method.
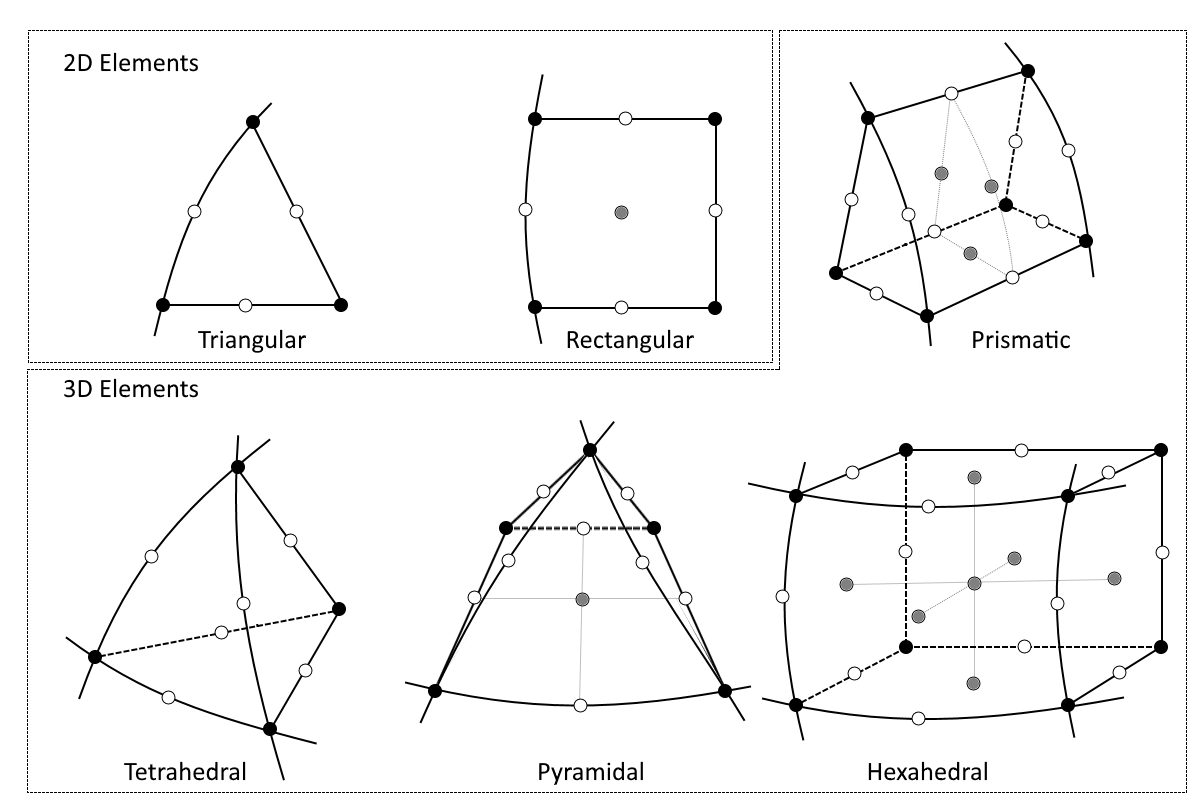
Lagrange elements with their node placement.
Additional Reading
There are so many advancements in mathematics and science that grew from Lagrange’s work; it’s impossible to cover them all in this blog post. If you’re interested in learning more, be sure to check out the links below.
- Learn more about Lagrange from these resources:
- Get a more in-depth look at the Lagrangian method:
- Learn more about some of Lagrange’s contemporaries on the COMSOL Blog:



Comments (0)