Introducing the Porous Media Flow Module

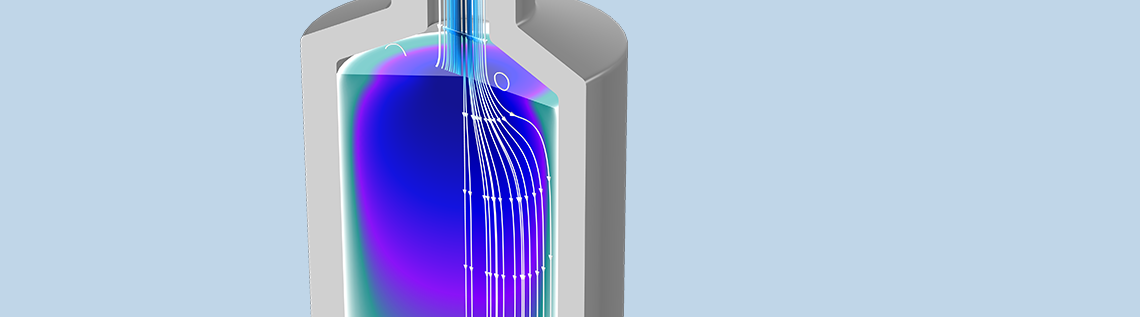
The need for advanced porous media modeling spans many industries. The Porous Media Flow Module, an add-on to the COMSOL Multiphysics® software available as of version 5.5, was made for this: It lets you quantitatively investigate mass, momentum, and energy transport in porous media. Interest areas for this product include fuel cell processes, pulp and paper drying, the production of food, filtration, and many more.

Modeling Porous Media Flow

Simulating mass, momentum, and energy flow in porous media is common in a number of engineering fields, such as chemical, civil, and nuclear engineering. The Porous Media Flow Module provides a comprehensive set of physics interfaces to help engineers and scientists simulate different types of physical processes in porous media.

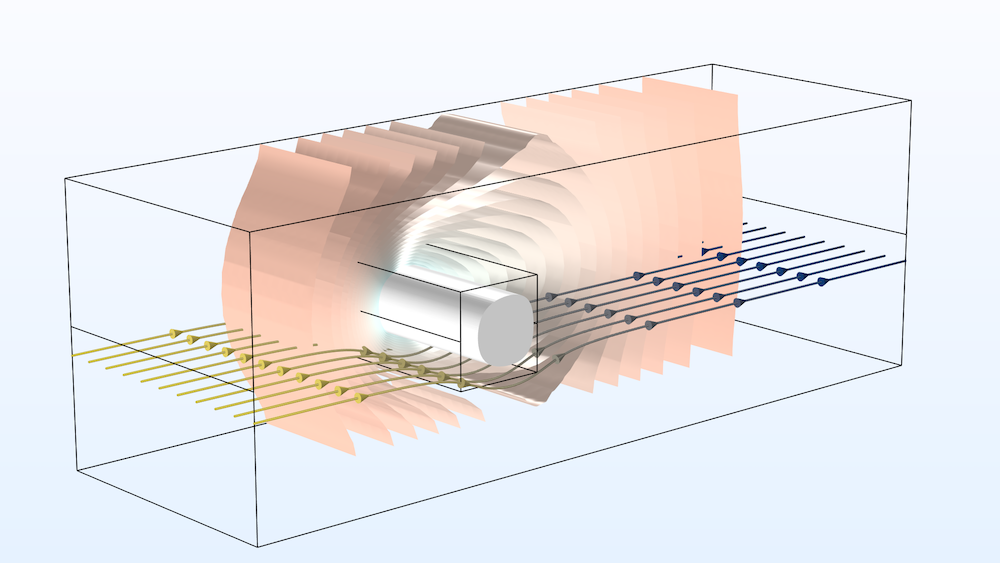
A frozen inclusion modeled using the Porous Media Flow Module.

The Porous Media Flow Module allows engineers within many different industries, such as mining, biomedicine, and the food industry, to analyze and optimize their processes in a user-friendly environment. Applications such as multiphase transport in porous media can be addressed within a fully multiphysics approach.

With the multiphysics capabilities of the Porous Media Flow Module, you can compute:

• Nonisothermal flow in a porous medium
• Effective properties for a multicomponent system
• Poroelasticity
• The transport of moisture and chemical species

Let’s take a look at a few of these application areas in more detail…

Multiphase Transport in Porous Media

The Porous Media Flow Module includes tools that can be used to simulate multiphase flow in porous media with two or any number of moving phases. You can specify porous media properties such as relative permeabilities and capillary pressures between phases to model wicking, moisture transport, or other transport phenomena in porous media.

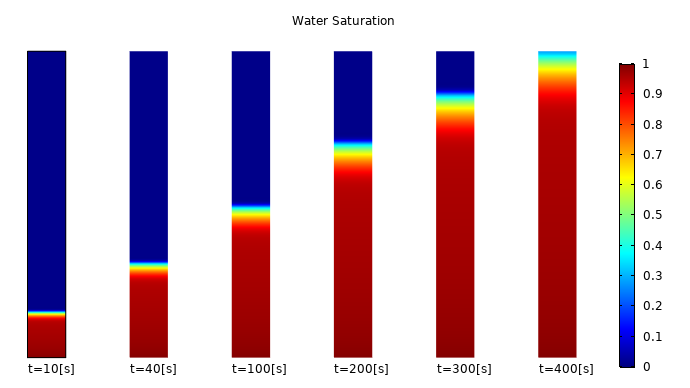
A model showing wicking in a paper strip, a porous medium.

When a dry strip of paper is put into contact with a fluid, it will absorb it due to capillary forces. Absorption will continue until gravitational forces balance the capillary forces. In this example, two phases, water and air, interact through the combination of the Darcy’s Law and Phase Transport in Porous Media interfaces.

Non-Darcian Flow in Porous Media

In a previous blog post, we discuss physics interfaces available for simulating flow in saturated and variably saturated porous media, including the Darcy’s Law and Brinkman Equations interfaces.

Darcy’s law applies to low interstitial velocity in the pores, which typically means Reynolds numbers below 100. For higher velocities and Reynolds numbers, an additional nonlinear correction can be added to the momentum equation. The Porous Media Flow Module includes the possibility to model non-Darcian flows, where the velocity field is nonlinear with respect to the pressure drop.

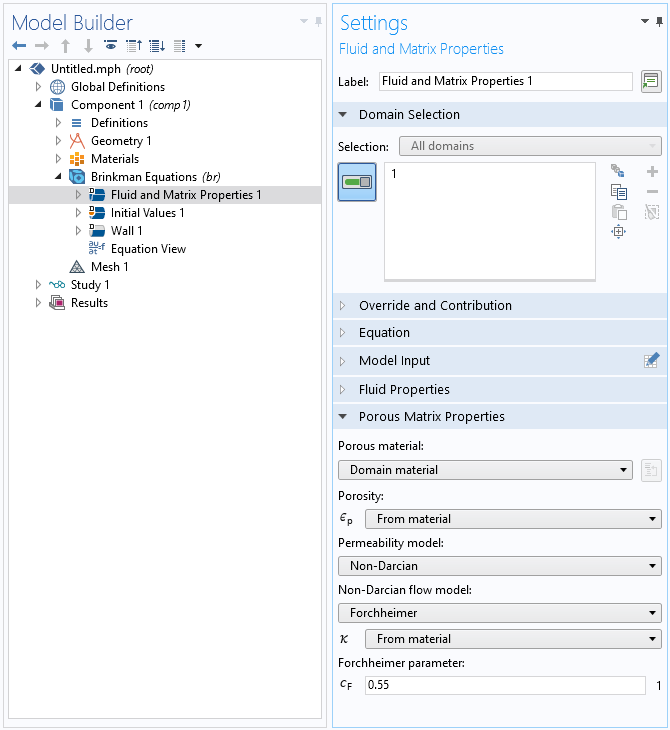
The available options to model non-Darcian flow in porous media are the Forchheimer, Ergun, Burke–Plummer, and Klinkenberg models for the Darcy’s Law and Multiphase Flow in Porous Media interfaces; and Forchheimer and Ergun models for Brinkman equations.

Local Thermal Equilibrium and Nonequilibrium for Heat Transfer in Porous Media

Heat transfer in porous media may occur due to conduction, convection, and dispersion, and it must take into account the different thermal properties of solid and fluid phases. With the Porous Media Flow Module, it’s possible to model heat transfer in porous structures using two modeling approaches:

1. Local thermal equilibrium (LTE), where the temperature of the solid matrix and the fluid phase are in local equilibrium
2. Local thermal nonequilibrium (LTNE), where distinct energy equations are formulated for the solid and fluid phases, and it is important to take into account for the heat transfer at the fluid-solid interface

A model of a packed bed latent heat storage unit including phase change effects and local thermal nonequilibrium.

Fracture Flow in Porous Media

Modeling mass momentum and energy transport in fractured porous media is relevant to chemical, civil, and nuclear engineers, to name a few. The Porous Media Flow Module includes physics interfaces to model pressure, temperature, and chemical species transport on internal boundaries within a porous matrix. This approximation saves you from meshing the actual fractures and the computational resources this entails.

A model of a ceramic water filter with an activated carbon core.

Ceramic water filters are commonly used to remove chemicals and particles from drinking water. The small pores in the ceramic core remove large particles and bacteria, and the activated carbon can also remove heavy metals and chlorine. Cracks in the ceramic core might result in remaining pollutants in the drinking water.

Phase Change in Porous Media

The Porous Media Flow Module also includes a tailored interface to model phase change in porous media. Typical phase transition phenomena include the melting of ice into water or the evaporation and condensation of vapor in building materials.

Next Step

Find out more about the dedicated functionality for modeling mass, momentum, and energy transport in porous media in the Porous Media Flow Module by clicking the button below: