
One of the questions we get asked all the time is: “Can I use COMSOL Multiphysics for solving my fluid-structure interactions problems?” Of course the answer is yes, so let’s talk a little about the various fluid-structure interaction (FSI) modeling techniques. Along the way, we will introduce the add-on modules you will need for these various types of analyses.
The Various Types of Fluid-Structure Interaction Modeling
Very broadly speaking, whenever you are modeling a problem that involves computing the velocity and/or the pressure field in a fluid as well as the stresses and strains in a solid material interacting with that fluid, you are solving a fluid-structure interaction (FSI) model.
Flow Around a Cylinder
When modeling an FSI problem, there are various assumptions that we can make to simplify the modeling complexity and reduce the computational burden. To get us started, let’s look at the most complete FSI model that you can build in COMSOL Multiphysics: the fluid flow around a cylinder.
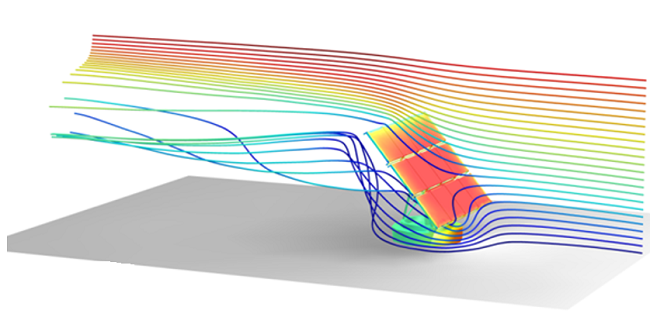
Deformation of a flexible object in the wake of a cylinder in crossflow.
The fluid wake behind the cylinder induces large oscillations in the solid protruding from the back of the cylinder. Solving this type of model requires that we address three problems. First, the Navier-Stokes equations are solved in the fluid flow regions. Next, the displacements in the solids are computed. Finally, the deformation of the mesh in the fluid region is solved to account for the deforming region through which fluid can flow.
This nonlinear multiphysics coupling is handled with the Fluid-Structure Interaction interface that is available within the MEMS Module or the Structural Mechanics Module. Such models can be solved in either the time-domain or as a steady-state (time-invariant) problem.
The example above considers a linear relationship between the stress and strain in the solid material. If you would like to model materials with a nonlinear stress-strain relationship, such as a hyperelastic material model commonly used to describe rubbers and polymers, you will also want to use the Nonlinear Structural Materials Module.
Peristaltic pump: A roller pumps fluid along a flexible tube. Image credit: Veryst Engineering.
One-Way Coupled FSI
On the other hand, you may know ahead of time that the structural displacements will be relatively small, but the stresses may be significant. You can still use the Fluid-Structure Interaction interface in this case, but instead also use a One-Way Coupled solver, which will compute the flow solution and apply the fluid loads onto the structural problem. That way, you will avoid computing the deformation of the mesh.
It is also possible to put together this type of one-way coupled FSI problem from scratch, without using the Fluid-Structure Interaction interface at all. This is demonstrated in the Fluid-Structure Interaction in Aluminum Extrusion example. Additionally, if you are dealing with a very high-speed flow and are not interested in the short time-span chaotic oscillations in the flow, then you can use a turbulent fluid flow model as part of your FSI model. Both the CFD Module and the Heat Transfer Module include various turbulence models appropriate for different flow regimes.
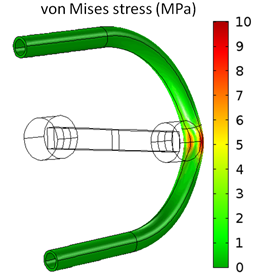
Solar Panel in Periodic Flow: The turbulent air flow around a solar panel and the resultant structural stresses are computed.
Vibrating Structure in a Fluid
If you know in advance that you are dealing with a vibrating structure in a fluid, then you can usually assume that the structural displacements will be relatively small. As a consequence, any induced bulk motion in surrounding fluid is negligible. However, since the structure is vibrating, a pressure wave will be excited in the fluid and sound will radiate away. Within the COMSOL software, this is handled via the Acoustic-Structure Interaction interfaces available in the Acoustics Module.
These interfaces assume that the variations in the displacements of the solids are relatively small and therefore do not induce significant bulk motion of the fluid, but only variations in the fluid pressure field. It is possible to solve such problems in the time-domain, but it can also be assumed that the displacements and pressure will vary sinusoidally in time. This allows us to model in the frequency domain, which is less computationally intensive to solve. Bulk losses due to fluid viscosity and material damping can be included.
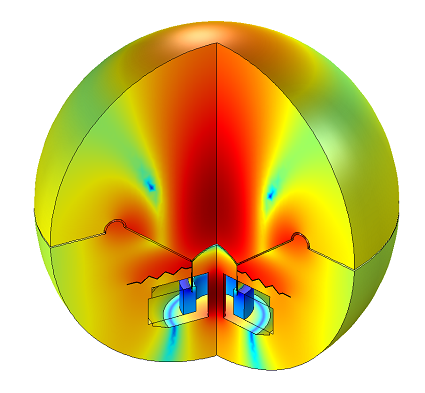
The sound pressure level radiated by a loudspeaker.
It is further possible to solve a Thermoacoustic-Solid Interaction problem, which solves a linearized frequency-domain version of the Navier-Stokes equations and can consider losses in the explicitly modeled thermal and viscous boundary layers. Although this is more computationally expensive than an acoustic-solid interaction problem, it is still much more efficient than solving the full FSI problem.
Vibrating Micromirror: The stresses and displacements of a vibrating micromirror and the surrounding air velocity.
Poroelastic Media
The Acoustics Module can also handle wave propagation through poroelastic media, such as wetted soils, biological tissues, and sound-damping foams using the Poroelastic Waves interface. This solves for both the structural displacements as well as the pressure of the fluid in the pores of the solid. An example is computing the reflection of a sound wave off an interface between water-sediment interface.
If you are interested in modeling poroelastic media, but in the steady-state or time domain instead of the frequency-domain, then you will need the Subsurface Flow Module. It is meant for modeling the steady-state or transient pressure-driven flow and static stresses in soils and other porous media. This module contains a Poroelasticity interface, so you can model poroelastic fluid-structure interaction in the steady-state and transient regime.
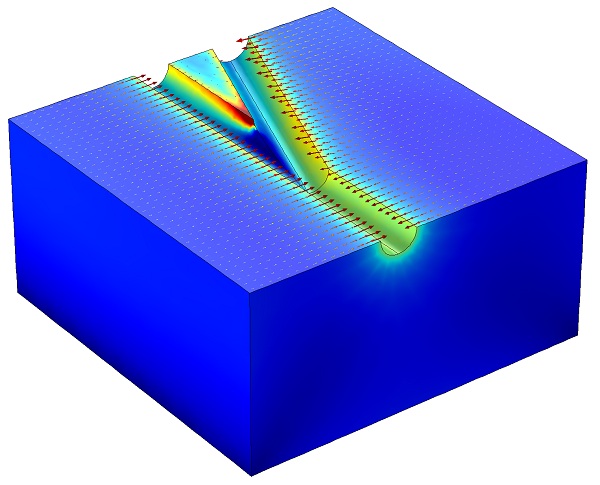
Open Hole Multilateral Well: The stresses in the soil and the fluid velocity in the poroelastic domain are plotted.
Thin Layers of Fluid and Pipe Flow
All of the approaches I just described explicitly model the volume of the fluid and solve the velocity and/or the pressure throughout these volumes. In circumstances where we have thin layers of fluid, such as in a hydrodynamic bearing, we can avoid a volumetric model of the fluid entirely and solve the Reynold’s equation, which solves only for the pressure in a thin film of fluid.
In this approach, we only solve for fluid flow along a boundary of the domain. This interface is available in the CFD Module and the MEMS Module. We can even take things further and only solve for the fluid flow along a line. In other words, we can solve for flow along a pipe using the Pipe Flow Module.
For an example of a model that considers both pressure variations along the length of a pipe as well as the effect of the elasticity of the pipe walls, please check out this example of solving the Water Hammer Equation.
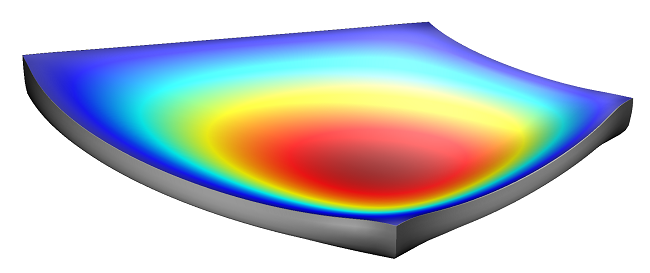
Tilted Pad Thrust Bearing: The pressure field in a lubricating layer and deformation of a tilted pad thrust bearing.
Taking Simplifying the Computations to the Next Level
You can probably see that we started with the most complex case and are looking at ways to simplify the computations, especially of the fluid flow field. Let’s take this to the extreme and consider the case of a fluid that isn’t moving at all, but does provide a hydrostatic pressure load on the structure.
Core Features
In such situations, we can take advantage of the core features of COMSOL Multiphysics: the User-Defined Equations, Component Coupling Operators, and Global Equations. These allow you to include an arbitrary equation into the model to represent any additional variable, such as fluid pressure. As we discussed in a previous blog post, you can include the effect of both a compressible and incompressible fluid within a deforming enclosed cavity, as well as the hydrostatic pressure.
Mixer Module
Now that we’ve introduced every way to simplify the fluid flow problem and compute the stresses, let’s finish up by turning things around and modeling the motion of a fluid for cases where we know the rigid body motion of the solid. Such situations can be handled via the Mixer Module, which is meant for addressing mixers and stirred vessels.
The motion of the solid structure is, in this case, completely defined via the rotation, and the movement of the fluid is computed. We can additionally compute the stresses in the moving solid objects, if we assume linear elastic deformations of the solids. This can be handled by a one-way coupled solution that first solves for the fluid flow field due to the moving mixer, and then computes the stresses under the assumption that the structural deformation is small.
Flow fields in a stirred mixing vessel.
Summary and Next Steps
As you can see, COMSOL Multiphysics is capable of handling a wide range of fluid-structure interaction modeling problems. If you’ve seen something here that you are interested in, or if there is something you’re curious about in this area that isn’t covered here, please contact us.







Comments (0)