
When most people think of a tuning fork, music comes to mind, since the device’s resonant frequency is used to tune instruments. As a MEMS practitioner, you’re more likely to think of a miniature gyroscope that can be formed by joining two tuning fork structures. Mass-produced MEMS gyroscopes provide affordable options for measuring angular velocity in applications such as yaw-rate sensors for skid control in automobile systems. We can test these designs and optimize their setup for mechanical systems using simulation.
The MEMS Gyroscope
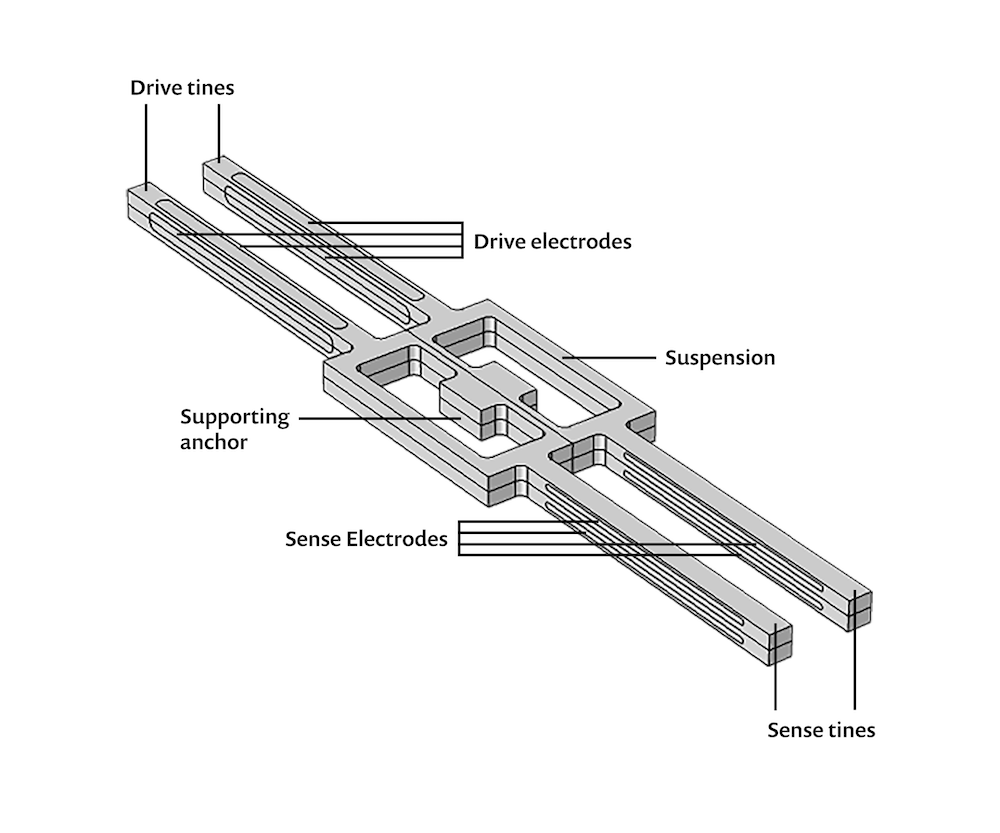
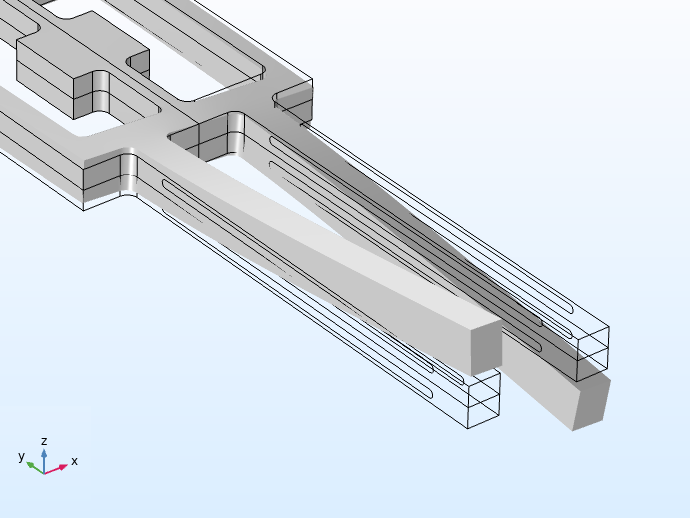
The MEMS device under consideration is essentially made up of two tuning forks working together to act as a rate gyroscope. These two elements are composed of piezoelectric materials. In the case of the model discussed here, the material is quartz.
A rate gyroscope senses the rotational motion and angular velocity of a system. In this piezoelectric rate gyroscope, the tuning forks’ resonant modes are used to produce the measurement signal.
Two resonant modes are used:
- Drive mode
- Sense mode
These two modes serve as the driving and sensing aspects of the gyroscope. In operation, the tuning fork is driven at the resonant frequency of the drive mode through an electric field applied by electrodes deposited on the surfaces of the drive tines. The drive tines vibrate in the tuning fork plane, the xy-plane. In the sense mode, the sense tines vibrate out of the tuning fork plane and along the z-axis instead. This displacement is shown in the set of images below.
The direction of displacement of the tuning fork prongs in drive mode (left) and sense mode (right).
The out-of-plane sense mode movement is caused by the effect of the Coriolis force as the gyroscope rotates around the y-axis. The reverse piezoelectric effect is used to drive the in-plane mode, while the out-of-plane motion is sensed by the direct piezoelectric effect.
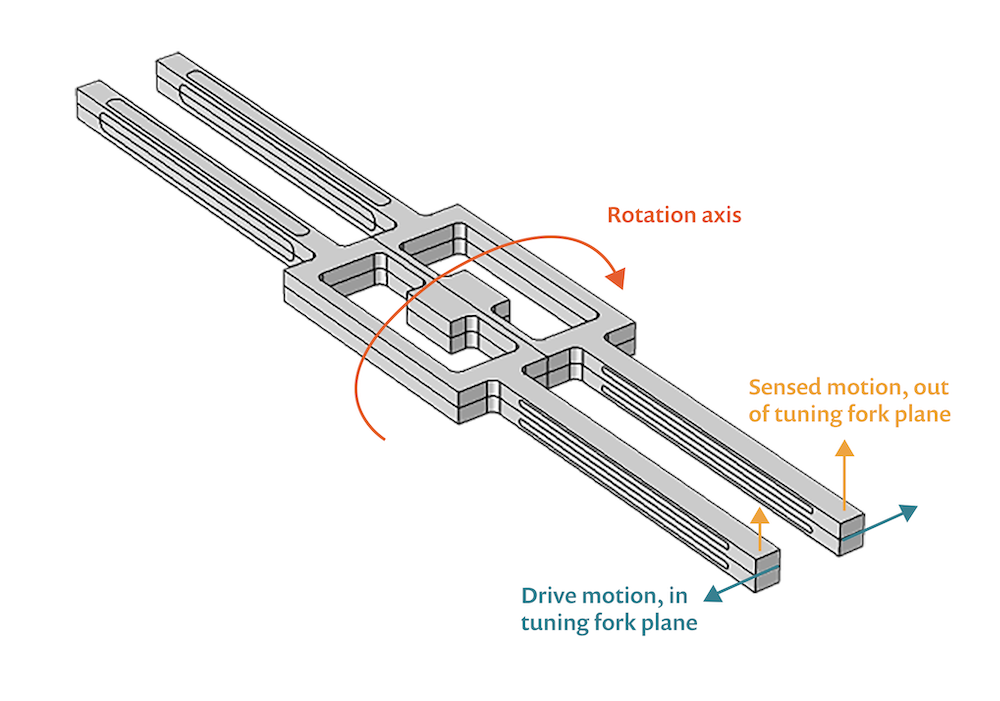
Essentially, these different parts work to help the system detect a skewed orientation as well as self-correct to a stable or balanced orientation. Balance helps to ensure safety and avoid damage in select mechanical systems, while achieving proper orientation in others. This ability is the reason MEMS gyroscopes are used in some skid control systems, as well as in rollover detection.
Setting Up the COMSOL Multiphysics® Model
As mentioned above, a piezoelectric rate gyroscope senses when a system is rotating. In this model, we simulate how the system operates through a simplified analysis.
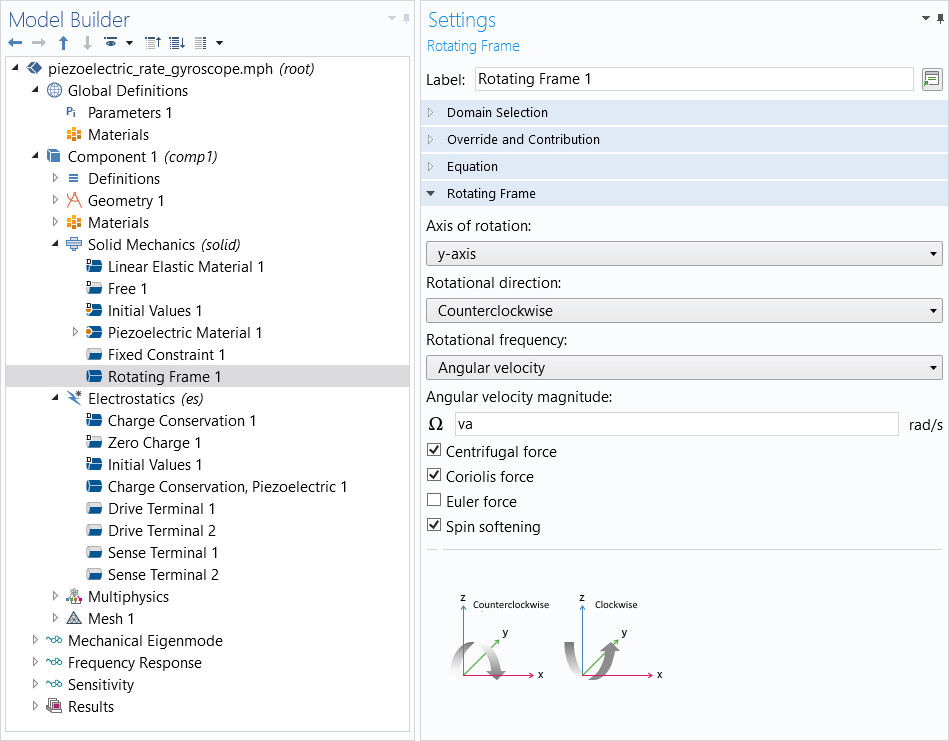
When modeling a piezoelectric rate gyroscope in the COMSOL Multiphysics® software, adding a rotating frame of reference accounts for the particular rotating body with which the device is mounted. This is done by adding the Rotating Frame node. Once you’ve established the properties for the frame of reference, you have the option to account for the Coriolis force by selecting the respective check box. The Coriolis force causes the tuning fork to vibrate in the out-of-plane motion of the sense mode.
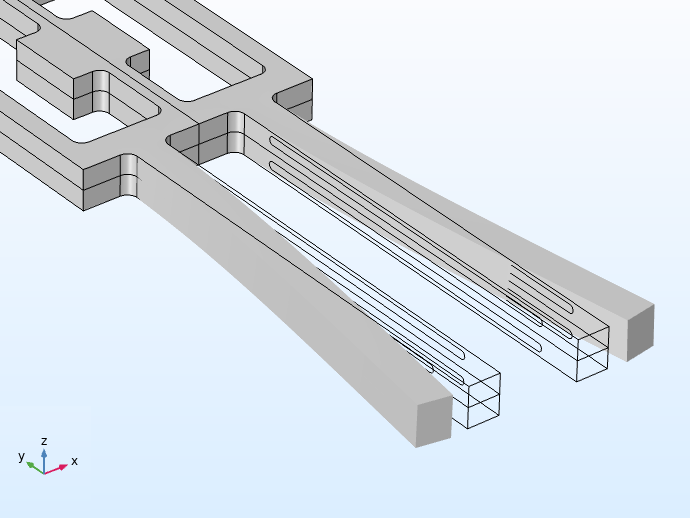
The electrodes on the tuning fork need to be patterned in specific ways with respect to the crystalline axes of the device’s piezoelectric material, quartz. This is important so that the drive tines are bent in the appropriate directions and the sense signals are isolated and extracted cleanly from the sense tines.
The Electrostatics physics interface provides the drive voltages and picks up the sense voltages through the electrodes. The electrodes create electric fields that drive the in-plane bending motion of the tuning forks’ tines. In the sense tines, the electrode pattern detects the out-of-plane motion of the sense mode. The structural mechanics and electrostatics are coupled through the Piezoelectric Effect multiphysics node.
Tip: When developing your model, it is sometimes advantageous to initially use a coarser mesh so that you get results quickly. You can then go back and create a finer mesh to generate more accurate results. When working with a coarse mesh, it helps to construct the geometry in a symmetrical fashion and use copy and paste functionalities to construct a symmetrical mesh, so that the symmetry of the physics is preserved numerically.
Results and Discussion
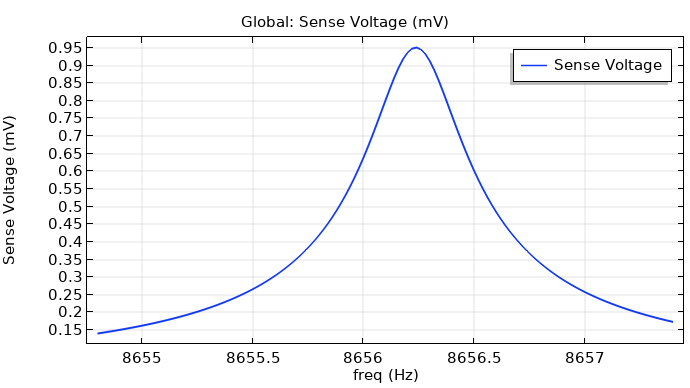
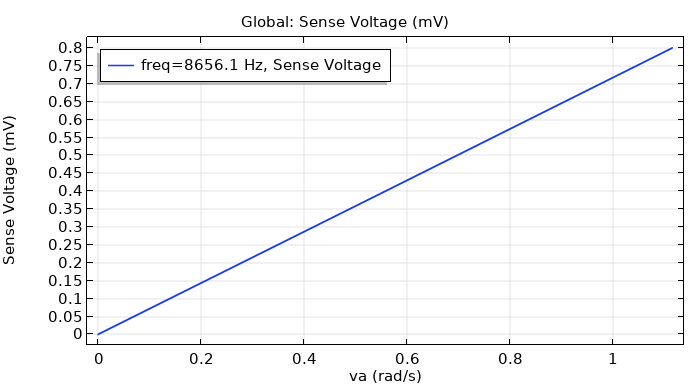
The results show how much the sense voltage changes for a given angular velocity as a function of the drive frequency, as well as the sense voltage at a fixed drive frequency as a function of the angular velocity.
Left: Sense voltage vs. drive frequency. Right: Sense voltage vs. angular velocity.
Simulation enables you to find the optimum design more efficiently, as you can adjust for any objective without the use of a prototype. With COMSOL Multiphysics, you can simulate real-life uses to test specific designs and optimize them for your specific system.
Try It Yourself
Try out the piezoelectric rate gyroscope tutorial model:




Comments (0)