Simulating the Pharmaceutical Tableting Process

People have used pills to treat illnesses for hundreds of years, with some references even dating back to ancient Egypt. It was not until the 19^th century, however, that the pharmaceutical tableting process was significantly modernized by William Brockedon and his machine patented for “Shaping Pills, Lozenges and Black Lead by Pressure in Dies”, which could compress powder into a tablet (Ref. 1). Today, powder compaction is widely used in the pharmaceutical industry due to its high flexibility, high material utilization, and better control over quality than other manufacturing methods.

In this blog post, we will explore the pharmaceutical tableting process using the Capped Drucker-Prager model available as of version 6.0 of the COMSOL Multiphysics^® software.

The Capped Drucker-Prager Model

The process of producing pharmaceutical tablets from powders, also known as tableting, consists of three main stages:

1. Die filling: The powder is delivered into a die cavity.
2. Compaction: The powder is pressed inside the die by an upper and lower punch to produce a tablet.
3. Ejection: The tablet is ejected from the die by the lower punch.

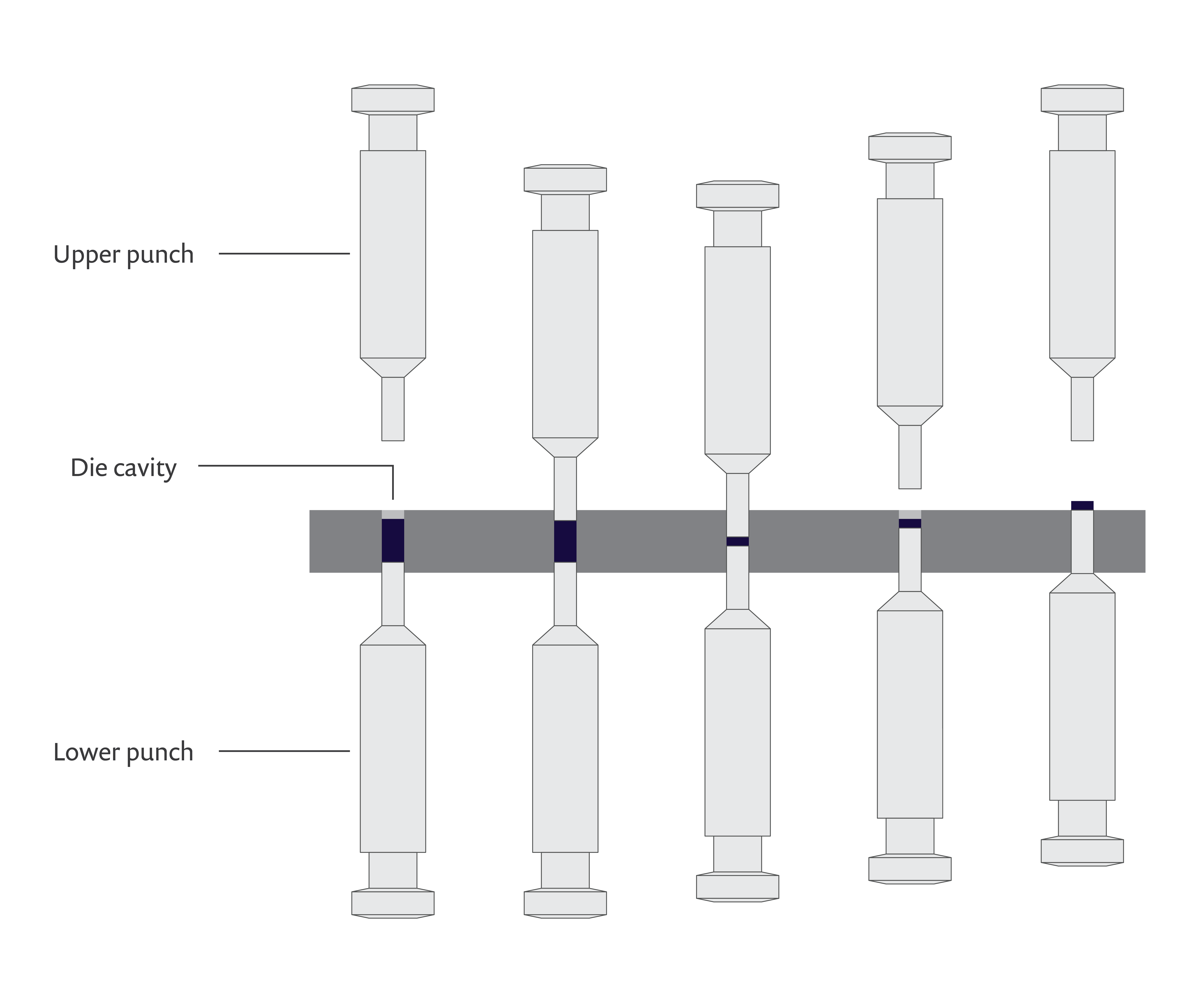
A schematic of the pharmaceutical tablet manufacturing process.

Using the Capped Drucker-Prager model, we will examine the compaction stage, evaluating the stress, strain, and density distributions of the mold as well as the effect of the punch force on axial compaction.

The constitutive material models used for finite element analysis of powder compaction processes can be divided into two main types:

1. Porous material models — for the compaction of medium- to low-porosity powder
2. Granular material models — for the compaction of high-porosity powder

The Fleck-Kuhn-McMeeking material model available in COMSOL Multiphysics is an example of a porous material model, while the Capped Drucker-Prager option is a granular material model. The Capped Drucker-Prager model is frequently used to simulate pharmaceutical powder compaction because the material parameters can be easily characterized and determined with experimental data. For the purpose of this example, the compaction of a high porosity powder known as microcrystalline cellulose (MCC) will be simulated using the Capped Drucker-Prager model. Note that the material properties are considered to be density dependent and the friction between the powder and the die is taken into account.

Note: If you are interested in learning how to simulate aluminum powder compaction using the Fleck-Kuhn-McMeeking and Gurson-Tvergaard-Needleman models in COMSOL Multiphysics, check out this blog post: Simulating Powder Compaction with Porous Plasticity Models.

Modeling Powder Compaction in COMSOL Multiphysics^®

Using the Nonlinear Structural Materials Module, an add-on to either the Structural Mechanics Module or the MEMS Module , we can begin our analysis by defining the geometry. The model geometry includes the workpiece — in our case, the microcrystalline cellulose (MCC) — and the die. The two punches that we need for the model setup are a fixed lower punch and an upper moving punch. The lower punch is modeled as a fixed axial displacement on the bottom boundary of the workpiece, and the upper punch is modeled by a prescribed displacement in the axial direction. Due to the rigid character of the die, it is not modeled explicitly.

More information on the setup of this model is available in the model’s documentation. For the purposes of this blog post, however, we will jump right into the simulation results.

Simulation Results in COMSOL Multiphysics^®

In order to evaluate the properties of the powder, let’s discuss the simulation results. At the beginning of the compaction process, the von Mises stress is higher on the top surface, profiling a large stress gradient in the workpiece. As compaction proceeds, the stress gradient reduces, and we can observe a lower stress ring at the bottom.

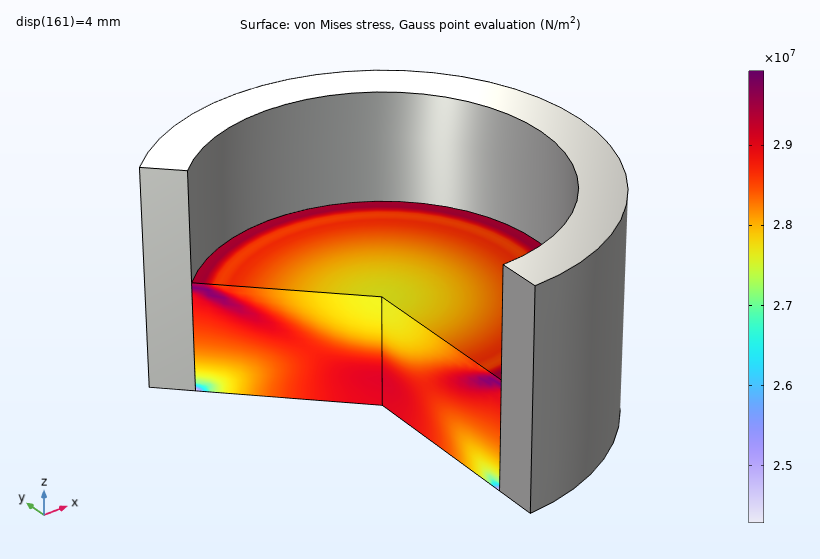
The von Mises stress at the end of the compaction process.

The plot below shows the volumetric plastic strain at the end of the compaction of the powder. We can see that there is a large variation in the volumetric plastic strain from the bottom face to the top face. The maximum compressive plastic strain occurs at the top.

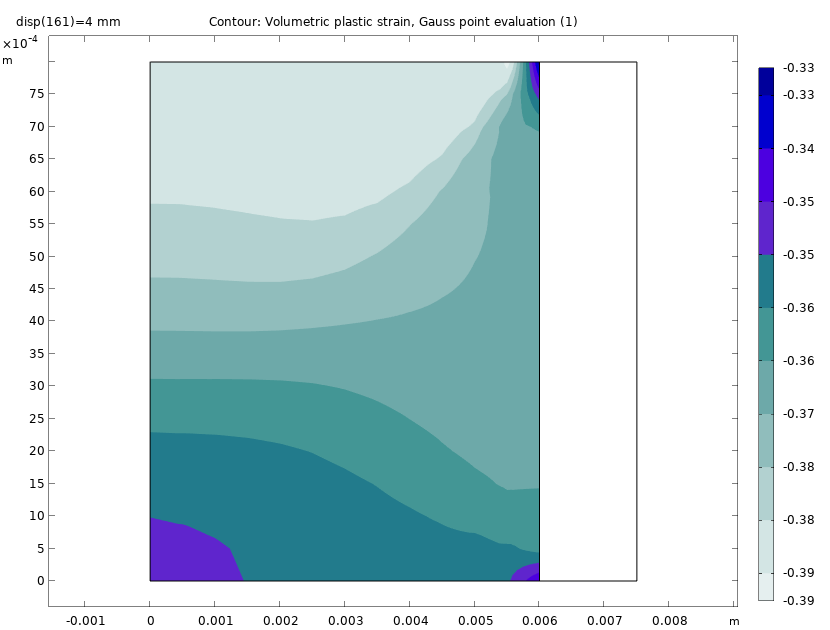
Volumetric plastic strain at the end of the compaction process.

The relative density distribution at different stages of the compaction can also be easily evaluated. Throughout all stages of compaction, the high density zone forms at the top end while a low density zone forms at the bottom end until the density reaches the final density of the tablet at the end of the tableting process. A nonuniform density can be observed in the powder mold due to the friction.

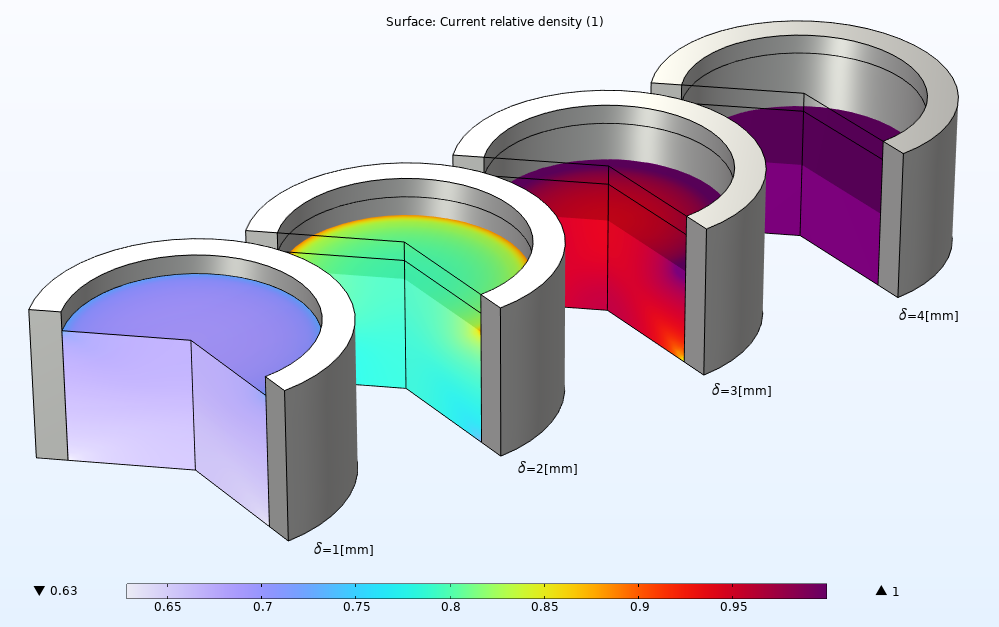
An array of four powder compaction plots showing the relative density at different stages of a pharmaceutical tableting process.

Lastly, our simulation results also show the punch forces versus the axial compaction in the powder compaction process. We see that the yielding occurs at the very early stages of the process.

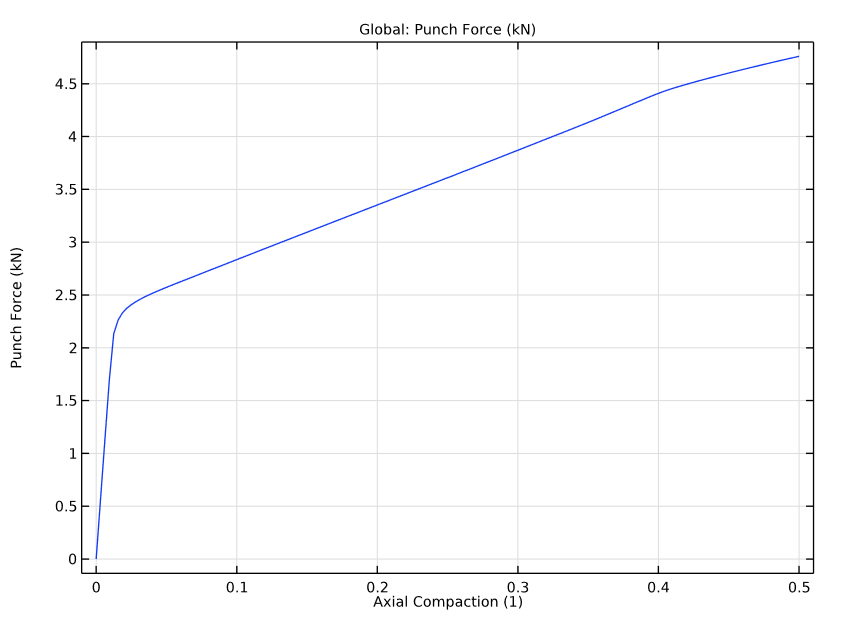
Punch force versus axial compaction.

Final Thoughts

In this blog post, we examined how to model the pharmaceutical tableting process in the COMSOL^® software. We used one of the most popular models for simulating compaction processes of pharmaceutical powders: the Capped Drucker-Prager model, which is often favored for modeling pharmaceutical powder compaction because it is able to represent various phenomena related to the compaction process. To get acquainted with the pharmaceutical powder compaction process yourself, try out the Pharmaceutical Tableting Process tutorial model:

Further Resources

• If you would like to further practice your simulations skills, you can check out these related tutorial models:
  • Two-Stage Powder Compaction Process
  • Powder Compaction of a Rotational Flanged Component
  • Powder Compaction of a Cup, combining the Fleck-Kuhn-McMeeking model with the Gurson-Tvergaard-Needleman model

References

1. “Tablet (pharmacy),” Wikipedia, Wikimedia Foundation, 15 July 2022; https://en.wikipedia.org/wiki/Tablet_(pharmacy)
2. A. Baroutaji, S. Lenihan, and K. Bryan, “Combination of finite element method and Drucker-Prager Cap material model for simulation of pharmaceutical tableting process,” Material Science and Engineering Technology, vol. 48, no. 11, 2017.
3. L. H. Han et al., “A modified Drucker-Prager Cap model for die compaction simulation of pharmaceutical powders,” International Journal of Solids and Structures, vol. 45, pp. 3088–3106, 2008.