|
| Filename | Size |
|---|---|
| CDE_uwDG.mph | 927 KB |
| CDE.png | 201 KB |
| up_dG_CDE.png | 115 KB |
| Download all files (Zip-archive) | ~ 993 KB |
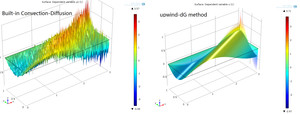
Convection dominated Convection-Diffusion Equation by upwind discontinuous Galerkin (dG) method
Huashan Sheng (盛华山), Department of Mathematics, Shanghai JiaoTong University (上海交通大学数学系)
Email:
We consider the Convection-Diffusion Equation with very small diffusion coefficient $\mu$:
\[
-mu\Delta u + \mathbf{\beta}\dot\nabla u =f \mathrm{in}~ \Omega
u=g(x,y) \mathrm{on}~ partial\Omega
\]
First we use the Convection-Diffusion Equation function of The Classical PDE Interfaces in COMSOL 4.4.
Then, we use the WeakForm PDE function and choose shape function type to be discontinuous Largrange.
We compare these two solutions.
Key functions : up() down() nx ny WeakForm PDE
Solving by COMSOL 4.4
User Comments
|
Aug 26, 2016 at 1:27pm UTC |
|
Thank you for sharing |
Login to comment on this entry.



