A Silicon Quantum Dot in a Uniform Magnetic Field
Application ID: 88981
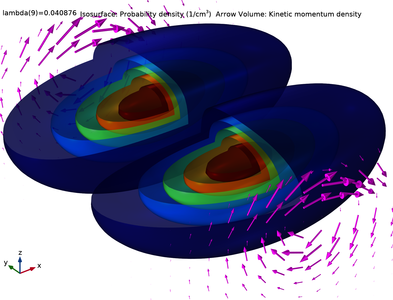
This tutorial model solves a two-component Schrödinger equation for the eigenstates of a simple silicon quantum dot in a uniform magnetic field, based on the paper by Jock et al. on the topic of spin-orbit qubits. The built-in domain condition Lorentz Force for the Schrödinger Equation interface is used to account for the contribution to the kinetic momentum from the vector potential. The coupling of the spin-up and spin-down components is implemented using the built-in domain condition Zeroth Order Hamiltonian. Together with the benchmark model k dot p Method for Strained Wurtzite GaN Band Structure, these examples show how to set up multiple wave-function components with the Schrödinger Equation interface. The computed probability density and kinetic momentum density of the ground state compare well with Supplementary Figure 1 in the paper. In addition, the computed energy difference between the first two eigenstates agrees well with the expected value from an intuitive analytic calculation.
This model example illustrates applications of this type that would nominally be built using the following products:
however, additional products may be required to completely define and model it. Furthermore, this example may also be defined and modeled using components from the following product combinations:
The combination of COMSOL® products required to model your application depends on several factors and may include boundary conditions, material properties, physics interfaces, and part libraries. Particular functionality may be common to several products. To determine the right combination of products for your modeling needs, review the Specification Chart and make use of a free evaluation license. The COMSOL Sales and Support teams are available for answering any questions you may have regarding this.
