Gross–Pitaevskii Equation for Bose–Einstein Condensation
Application ID: 52221
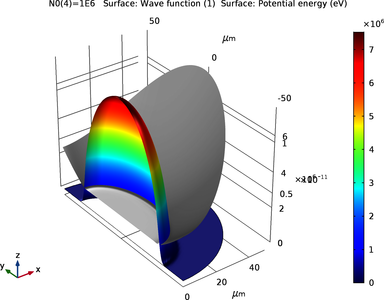
This tutorial model solves the Gross–Pitaevskii Equation for the ground state of a Bose–Einstein condensate in a harmonic trap, using the Schrödinger Equation interface in the Semiconductor Module. The equation is essentially a nonlinear single-particle Schrödinger Equation, with a potential energy contribution proportional to the local particle density. The eigenvalue study is not suitable for solving this kind of nonlinear eigenvalue problems. Instead, a stationary study is used with a global equation enforcing the normalization of the wave function to solve for the ground state solution. The result for a large number of particles compares well with the Thomas–Fermi approximation as expected.
This model example illustrates applications of this type that would nominally be built using the following products:
however, additional products may be required to completely define and model it. Furthermore, this example may also be defined and modeled using components from the following product combinations:
The combination of COMSOL® products required to model your application depends on several factors and may include boundary conditions, material properties, physics interfaces, and part libraries. Particular functionality may be common to several products. To determine the right combination of products for your modeling needs, review the Specification Chart and make use of a free evaluation license. The COMSOL Sales and Support teams are available for answering any questions you may have regarding this.
