Technical Papers and Presentations

INTRODUCTION: This paper investigates the design of IPMSM as drive motor for an electric race car in the competition called Formula Student. A key parameter for electrical motor is the power density which is very important for the performance of such race vehicles [1] to keep the overall mass small at high power. Furthermore, to run the motor at high power and to prevent it from overheating due to electrical and magnetic losses the motor and its power electronic are cooled in series[2]. In the design phase of the cooling system the knowledge of the component losses is very important. The overall goal of the project is a flexible motor design that can be adapted to new design constraints. In order to keep the development time short, it is useful to get a reliable prediction of the motor losses with the help of simualtion without having the physical motor for measurements [3]. For this work a predefined motor design will be used. The electromagnetic design of the used motor is given in [4] . Based on this concept, the losses and the heating behavior are evaluated in a FEM-model for different operating points, using COMSOL Multiphysics®.

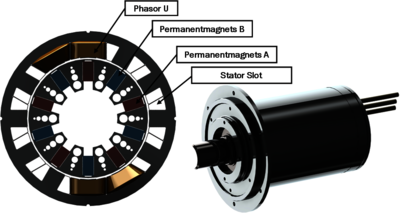
USE OF COMSOL Multiphysics®: The simulated components and geometry are shown in Figure 1. It corresponds to a motor variant which is currently designed by the Augsburg Student racing Team [2]. The simulation model setup is based on the Rotating Machinery Magnetic and Heat Transfer interfaces. For the material properties, nonlinear H-B characteristics are used for the rotor and stator iron. The model is modified to investigate the losses related to the electromagnetic induced iron losses[3].

RESULTS: The simulation visualizes the losses according to the electrical inputs, current and voltage, and the electrical frequency. As well as the losses the heating behavior is investigated to forecast the spots with elevated temperatures.