Happy Birthday, Olga Ladyzhenskaya

Olga Ladyzhenskaya started out as what some might call a child prodigy. She had a keen interest in math from a young age and devoted herself to the subject ever since. Her area of interest? Partial differential equations (PDEs), specifically the complex Navier–Stokes equations. She wrote several popular books (and over 200 articles) on PDEs, which have all helped earn her the title of one of the most influential mathematicians of the 20^th century.

A Life Devoted to Numbers

Olga Ladyzhenskaya was born on March 7, 1922, in Kologriv, a rural Russian town. From a young age, she loved reading and solving complex math equations. Ladyzhenskaya gained a strong appreciation for numbers and algebra from her father, who was a mathematician, high school principal, and math teacher.

At age 15, Ladyzhenskaya’s life changed forever when her father was arrested and killed by Soviet authorities. At the time, the authorities called him an enemy of the state, but he was posthumously exonerated in 1956. After her father’s death, Ladyzhenskaya devoted a majority of her time and energy to the field of mathematics.

Olga Ladyzhenskaya. Image by unknown — Math.ru. Licensed under CC BY-SA 4.0, via Wikimedia Commons.

At her high school in Kologriv, Ladyzhenskaya excelled in her classes and graduated with honors. However, she was denied from attending the university of her choice because of her father’s political status. Instead of going to school, she began teaching math at an orphanage and high schools in the area.

Her road to higher education finally began in 1943 when she was accepted to Moscow State University. While there, she learned from a handful of elite mathematicians, like Israel Gelfand and Ivan Petrovsky. In her third year, Ladyzhenskaya joined a three-student seminar taught by Gelfand, where each student was expected to work on an intricate math problem. Mark Vishik, a gifted mathematician and fellow student in the seminar, said this of Ladyzhenskaya:

“Ladyzhenskaya got the problem of describing the domain of an elliptic operator of the second order with Dirichlet boundary conditions and with the right-hand side belonging to L₂(Ω). She proved that if this boundary-value problem has a unique solution, then the elliptic operator is an isomorphism between the Sobolev space H²(Ω) ∩ H₀¹(Ω) and L₂(Ω). She also found an estimate for the norm for the corresponding inverse operator.”

After graduating from Moscow State University, Ladyzhenskaya went on to receive doctorates from both Leningrad State University (now known as Saint Petersburg State University) and Moscow State University, respectively.

Moscow State University in 2002. Image by Ivtorov — Own work. Licensed under CC BY-SA 4.0, via Wikimedia Commons.

Ladyzhenskaya worked as a math professor in the physics department at Saint Petersburg State University and then went on to become the head of the Laboratory of Mathematical Physics at the Steklov Mathematical Institute in 1961.

Throughout her career, Ladyzhenskaya devoted herself to working on PDEs. Along with one of her students, Nina Nikolaevna Uraltseva, Ladyzhenskaya solved Hilbert’s 19^th and 20^th problems for a wide class of second-order PDEs.

She also wrote over 200 technical papers and several books that are still used when studying PDEs today, including:

• The Mixed Problem for a Hyperbolic Equation
• The Mathematical Theory of Viscous Incompressible Flow
• Linear and Quasilinear Elliptic Equations
• Linear and Quasilinear Equations of Parabolic Type
• The Boundary Value Problems of Mathematical Physics
• Attractors for Semigroups and Evolution Equations

Studying the Navier–Stokes Equations

Olga Ladyzhenskaya was always up for a mathematical challenge, so it’s no surprise that her favorite PDEs to study were the complex Navier–Stokes equations. These equations describe the motion of fluids and are considered extremely challenging to solve, because the solution becomes unsteady and seemingly random when turbulence arises. (In fact, the Clay Mathematics Institute currently offers a one-million-dollar reward to the first person who can demonstrate a proof of existence, smoothness, or breakdown of the Navier–Stokes equations.) Through her research, Ladyzhenskaya was able to prove the convergence of a finite difference method for the Navier–Stokes equations.

Today, the Navier–Stokes equations are integral to fluid flow modeling. They are used to model a variety of applications, like inkjet nozzles and centrifugal pumps, among other examples.

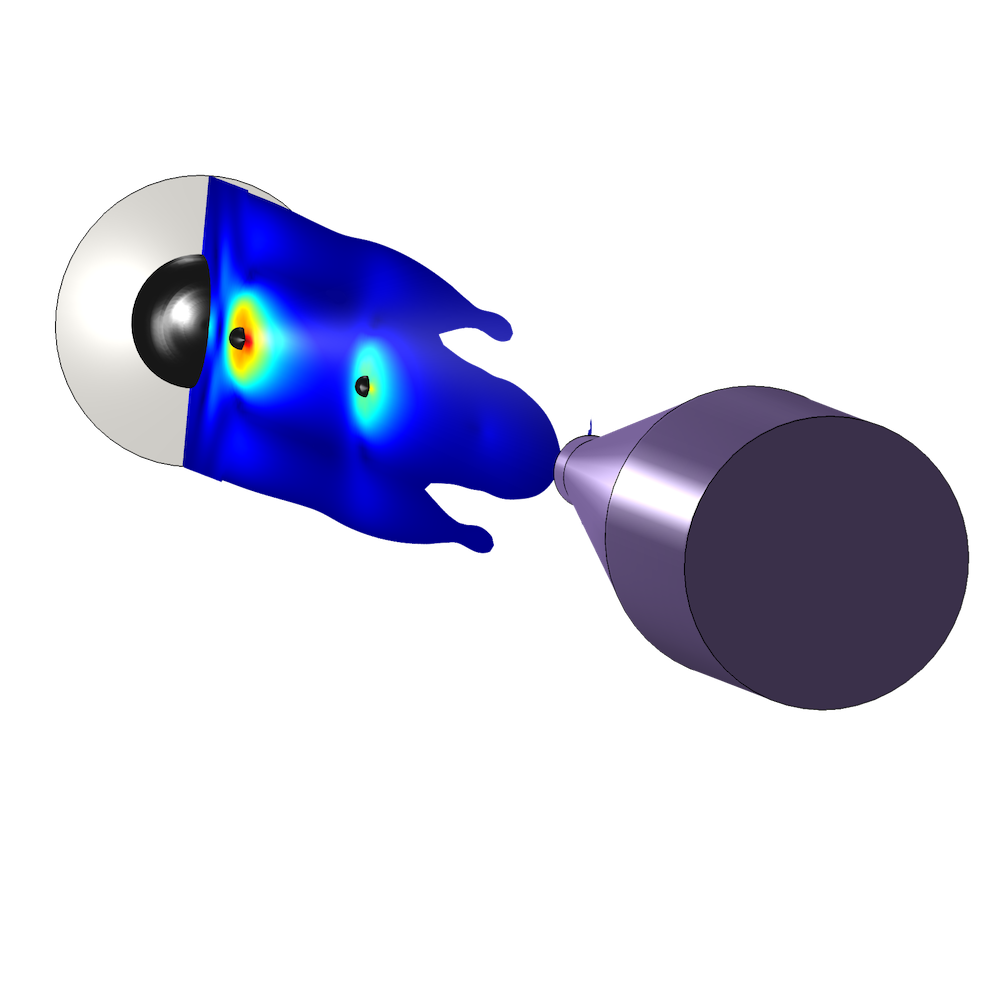
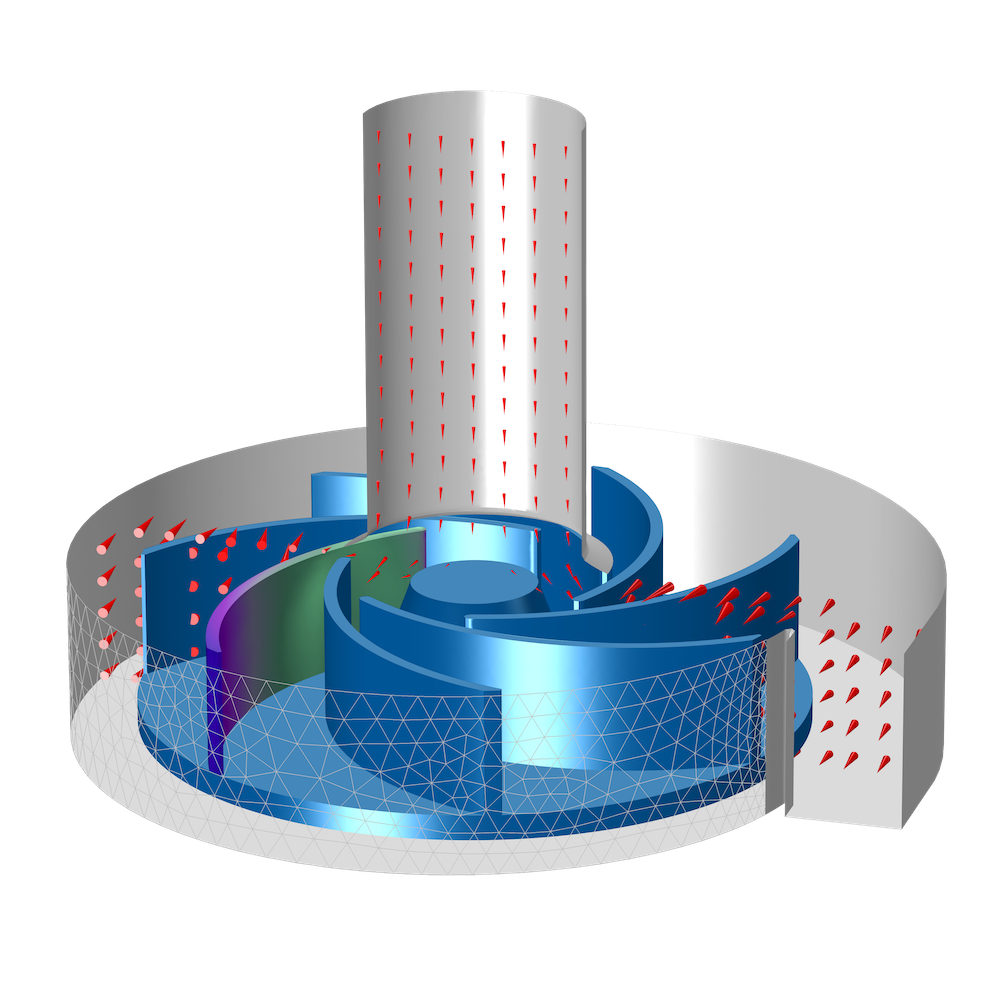
Simulations of an inkjet nozzle (left) and a centrifugal pump (right).

The Lasting Legacy of Olga Ladyzhenskaya

In 1981, Olga Ladyzhenskaya became a corresponding member of the Russian Academy of Sciences, and later became a full member in 1990. She was also awarded the Lomonosov Gold Medal by the Russian Academy of Sciences in 2002. At the Museum of Science in Boston, Massachusetts, you can find her name engraved on a marble desk as one of the top 20 most influential scientists of the 20^th century.

Museum of Science in Boston, MA. Image by Mysekurity — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.

Right before she passed away in January 2004, Ladyzhenskaya was still devoting herself to her work by analyzing the computational aspects of hydrodynamics. Her mathematical legacy lives on thanks to the numerous amounts of books and papers she authored and the brilliant minds she taught.

Today, let’s wish Russian mathematician Olga Ladyzhenskaya a happy birthday!

Further Reading

• Read more about Olga Ladyzhenskaya and her accomplishments from these resources:
  • The New York Times
  • American Mathematical Society
  • SIAM News
• Learn about other notable mathematicians with similar experiences:
  • Sir George Gabriel Stokes, a physicist and mathematician who helped form the Navier–Stokes equations
  • Sofia Kovalevskaya, a mathematician who contributed to differential equations, analysis, and mechanics