Introduction to Modeling Surface Reactions in COMSOL Multiphysics®

In biophysics, electrochemistry, and the design of catalytic reactors, researchers and engineers exploit the special chemical and physical properties of solid surfaces involving both gas-solid and liquid-solid interfaces. This blog post discusses the basics of the kinetics of surface reactions at simple surfaces and how they can be modeled with the COMSOL Multiphysics® software. In a subsequent blog post, we will look at how mass transport and reaction kinetics at surfaces are described for homogenized porous media.

Why Are Surfaces Special?

Surfaces are the locations for what chemists call heterogeneous reactions. These are reactions that involve more than one phase, such as in the catalytic reduction of nitrogen oxides at a solid surface in a catalytic converter. Because phases refer to different immiscible components of a system, heterogeneous processes can only take place at the interfaces where different phases meet.

Surfaces also act as sites for adsorption. This is a process in which a molecule in the adjacent gas or liquid phase becomes localized at the surface, either through intermolecular forces, like van der Waals forces (physisorption), or through a direct chemical bond (chemisorption). Adsorption can allow molecules from the gas and liquid phase to spend more time in close proximity (while they are stuck to the solid surface) than would be the case when they are in the free gas or solution. Also, chemisorption can lower the activation energy required to break chemical bonds in the adsorbed molecule, so that reactions between adsorbed chemical species can proceed through a different mechanism from the case in the free phase. These are two important reasons why solid surfaces can catalyze reactions.

Kinetics of Surface Reactions

The rate of a homogeneous reaction can be measured according to the number of moles of material that react per unit volume and per unit time; this sets the reaction rate in units mol m^-3 s^-1. By contrast, the rate of a heterogeneous reaction depends on the unit area that is available for a reaction, so the reaction rate is expressed in units mol m^-2 s^-1. These are units of molar flux. When setting up a chemical model in COMSOL Multiphysics, a direct way to specify a heterogeneous reaction is to add a Flux boundary condition.

We can imagine a flux of the reactant “into” the surface and, correspondingly, a flux of products “out of” the surface. The figure below illustrates the flux of a reactant measured into a catalytic surface.

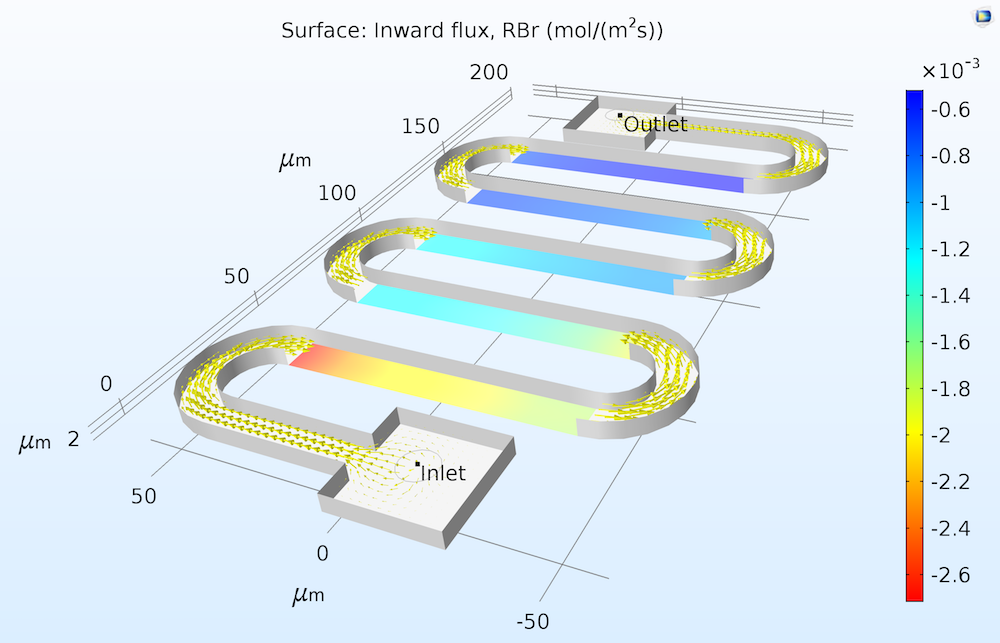
Flux of the solution-phase reactant RBr at a series of catalytic surfaces in a microreactor. Since the reaction consumes the RBr reactant, the inward flux to the solution is negative.

The rate of a surface reaction is expressed according to a rate law as a function of reactant and product concentrations as well as other local properties, such as temperature or pressure. Many of the same rate laws encountered for homogeneous reactions can also apply to heterogeneous reactions. If you’d like to review some different kinetic rate laws, take a look at this introductory blog post on chemical kinetics.

As an example of a rate law for a heterogeneous reaction, a first-order reaction consuming species A might set the following inward flux of A:

Here, N_A is the flux (mol m^-2 s^-1) and c_A is the concentration of the reactant located at the surface, but measured in the adjacent phase (mol m^-3).

Hence, the first-order rate constant has units m s^-1, representing an effective “velocity” of the chemical species into the boundary due to its reaction. It is common to find rate constants for surface processes, including those in electrochemistry, represented in units of velocity.

The Hydrocarbon Dehalogenation in a Tortuous Microreactor tutorial model is a good example of how surface processes are modeled. Here, two competing surface reactions are both active on specific catalytic surfaces represented by a Flux boundary condition in the Transport of Diluted Species interface. The respective rates of these processes are controlled by Arrhenius kinetics with different activation energies. Compared with the hydrogenation reaction, the competing dimerization reaction has a higher activation energy, hence it is accelerated more rapidly with an increasing temperature. The temperature dependence of the product ratios could be predicted with this model and compared with experimental data.

The image below shows a section of the Model Builder with the Flux boundary condition. As you can see, this condition applies specifically to the catalytic surfaces where the reactions take place. The reaction rates are defined using the kinetic mechanism specified in the coupled Chemistry interface. See the following section for more details on how this interface is used for surface reactions.

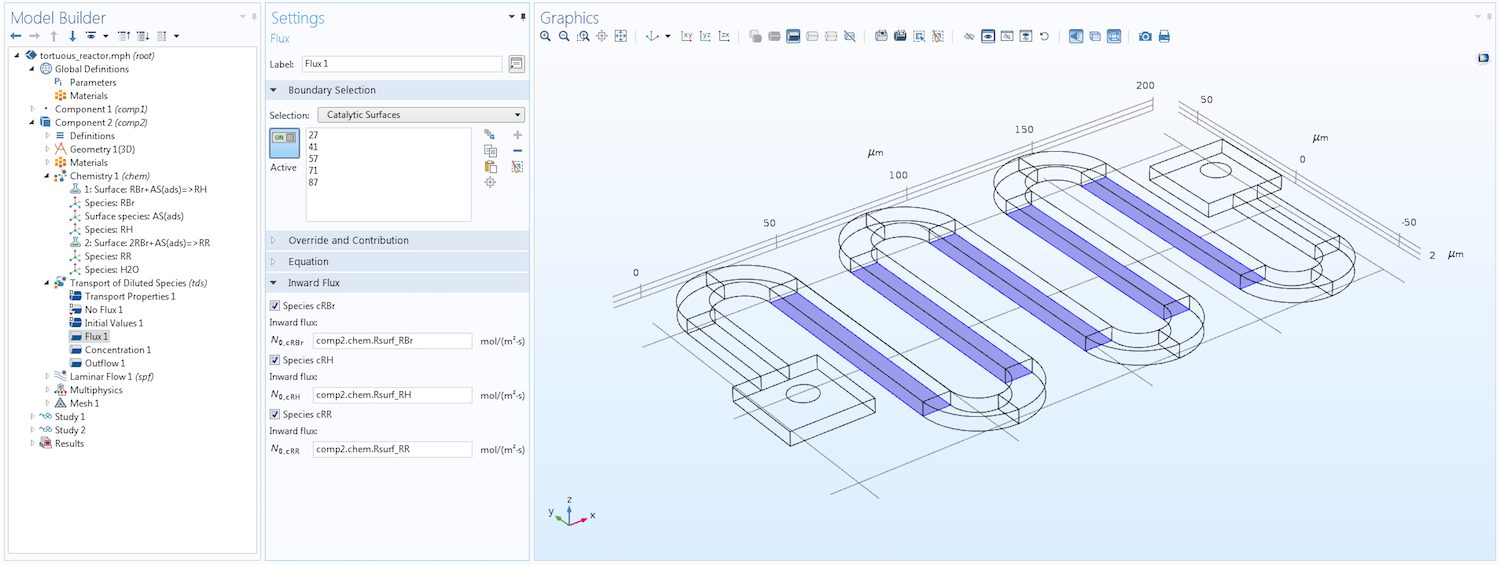
The Model Builder, showing the settings for a Flux boundary condition that defines the flux of three solute species at catalytic surfaces due to a heterogeneous reaction.

Adsorption and Transport at Surfaces

In an adsorption process, the flux of a chemical reactant into the surface is not balanced by a flux of a chemical reactant out of the surface. Instead, the surface concentration (mol m^-2) of the adsorbed reactant changes. Consider the adsorption of a chemical species from the gas phase. We can write this as an equation of the form: A(g) A(ads).

The conservation of mass can be expressed by writing:

This is a transport equation on the surface. The quantity N_ads is the flux of the adsorbed species tangent to the surface due to processes such as surface diffusion. In many cases, this surface diffusion is approximately zero. On the right-hand side, the flux acts as a reaction term to apply a source or sink of mass for the adsorbed species.

This equation is implemented in the Surface Reactions interface in COMSOL Multiphysics. Typically, it can be coupled to the Transport of Diluted Species or Transport of Concentrated Species interface for the mass transport in the adjacent gas or liquid phase. To see an example of the use of this interface, take a look at this blog post on modeling protein adsorption.

In this example, a section of an ion-exchange column is simulated to predict the rate of uptake of two protein species from a flow of an aqueous solution onto an active surface. The spherical ion-exchange beads are explicitly included in the geometry and the boundaries at their surface are used as the location for the adsorption reaction. The model includes four interfaces:

1. Chemistry interface for the chemical mechanism
2. Transport of Diluted Species interface for the concentrations of dissolved species in the flow (including heterogeneous reactions)
3. Surface Reactions interface for the surface concentrations of adsorbed species on the ion-exchange bead surfaces
4. Laminar Flow interface to predict the velocity field in the flow of water, hence the contribution of convection to transport of dissolved species

A typical plot is shown below, illustrating the adsorption extent after 30 seconds of exposure to the flow.

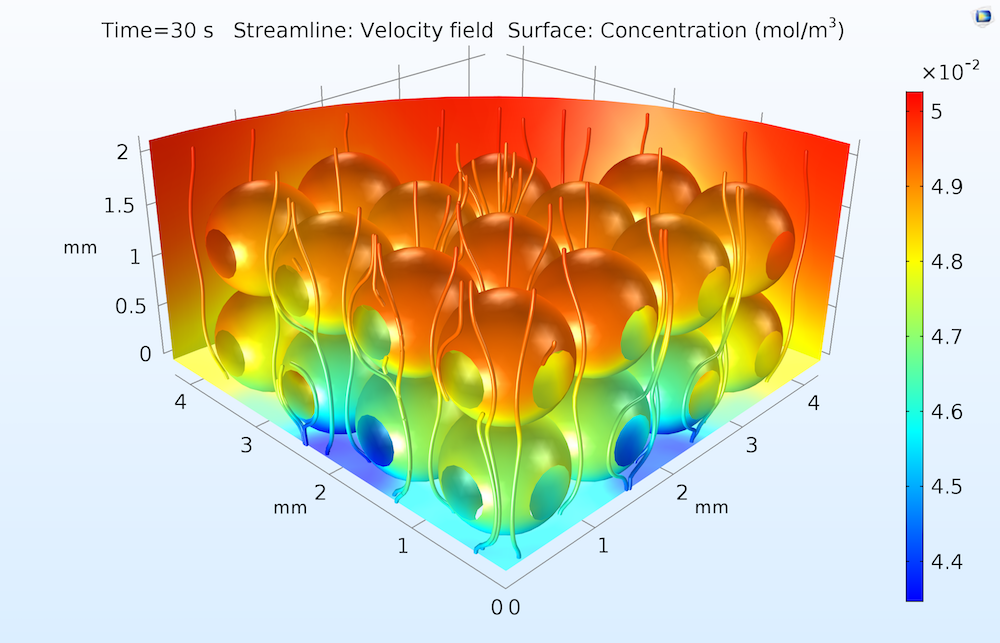
The surface concentration of an adsorbed protein in an ion-exchange column after 30 seconds of exposure to a flow of water containing the dissolved protein. Concentrations are higher toward the upper (inflow) face of the ion-exchange column, where the catalytic surfaces are more accessible to the dissolved protein in the flow.

Note that in this example, the surface diffusivity of the adsorbed species is set to zero. Therefore, the rate of change of the adsorbed species concentration at any point depends only on the local adsorption and desorption fluxes. The dynamic equilibrium between the kinetic adsorption and desorption processes is often described using a mathematical relation called an adsorption isotherm (one example is the Langmuir isotherm). We’ll discuss the choice and implementation of isotherms in more detail in an upcoming blog post in this series.

Defining Surface Reactions in the Reaction Engineering and Chemistry Interfaces

When using the Reaction Engineering interface to describe the behavior of a perfectly mixed reactor, surface reactions can be included by adding any surface-bound species to the reaction mechanism. Surface-bound species are indicated by the suffix (ads) at the end of a species name. Any reaction involving a surface species is understood to take place at a surface and thus has a reaction rate measured in mol m^-2 s^-1.

The option Generate Space-Dependent Model from a Reaction Engineering interface creates a Chemistry interface that stores the same mechanism as well as a Transport of Diluted Species interface or another chemical species transport interface for the bulk phase. The concentrations of adsorbed species are not traced by default, but you can add an extra Surface Reactions interface to do so.

There are two options for treating surface reactions. If they are assumed to apply at boundaries that will be explicitly resolved in the geometry of the space-dependent model, a Flux condition is added to the chemical species transport interface to describe the heterogeneous processes.

Fast reactions at surfaces can also be described with the help of a Surface Equilibrium Reaction feature. This constrains the concentrations of reactants and products at an interface to maintain a certain ratio, according to the equilibrium constant of a reaction. The screenshot below shows the Model Builder settings in the protein adsorption example.

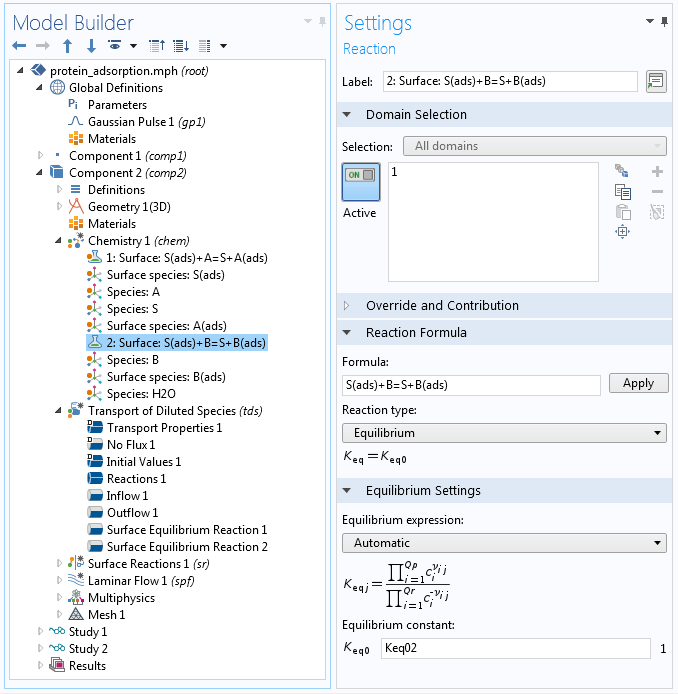
The Model Builder, showing the settings for a surface reaction within the specification of a kinetic mechanism through the Chemistry interface. The reaction is assumed to be very fast so that equilibrium according to a specified equilibrium constant is maintained.

Concluding Thoughts on Modeling Surface Reactions

In this blog post, we have introduced some basic kinetic theory for surface reactions as well as the conservation of mass between concentrations of species localized at a surface and concentrations of the same chemical species in an adjacent bulk phase (gas or liquid). The Flux boundary condition and Surface Reactions interface in COMSOL Multiphysics are used to add these reactions to chemical models. So far, we have only considered cases where the boundary has a simple shape so that it can be included in the geometry directly in order to define the location of surface reactions.

Stay tuned for the next blog post in this series, where we will discuss the theory of how reactions at the surfaces of porous media with complicated surface geometries can be approximated using homogenization.

Further Resources

• Learn more about modeling chemical reactions on the COMSOL Blog:
  • How to Model Heat and Moisture Transport in Porous Media with COMSOL®
  • Sensing the Bio in Biosensor Design with a Simulation App
  • Modeling Approaches in Heterogeneous Catalysis