
During routine exams, eye care professionals look for common refractive errors like nearsightedness, farsightedness, and astigmatism. As patients age, doctors also look for presbyopia, a loss of the accommodative amplitude that results long-term in a complete loss of the near vision. The visual accommodation process is complex, and useful eye properties needed to improve diagnosis and presbyopia treatment are difficult to obtain. To address the problem of measuring the refractive index of the lens, researchers developed a reverse engineering technique using simulation.
Focusing on Presbyopia Correction with Simulation
Presbyopia is an eye disorder that results in the loss of the near vision. The World Health Organization (WHO) says that “uncorrected presbyopia is the most common cause of visual impairment” — and it becomes more prevalent as we get older, with an onset at around 45 years old.
While we’re young, visual accommodation helps our eyesight to naturally adapt its distance of focus for far and near objects. Among other factors, the crystalline lens of the eye is able to change its shape through a complex biomechanical process that causes far vision to be passive and near vision to be active. However, as we age, geometric changes happen in the lens. The growth of the lens and the mechanical property change of the lens (the lens gets stiffer) cause the ciliary ring to be pushed forward. Lens compliance is affected more and more until the amplitude of deformation is almost nonexistent between far and near vision. The lens’ shape increases, and its equivalent refractive power and overall diameter decrease to the point that, in cases of presbyopia, the most accommodated shape ends up being the far vision.
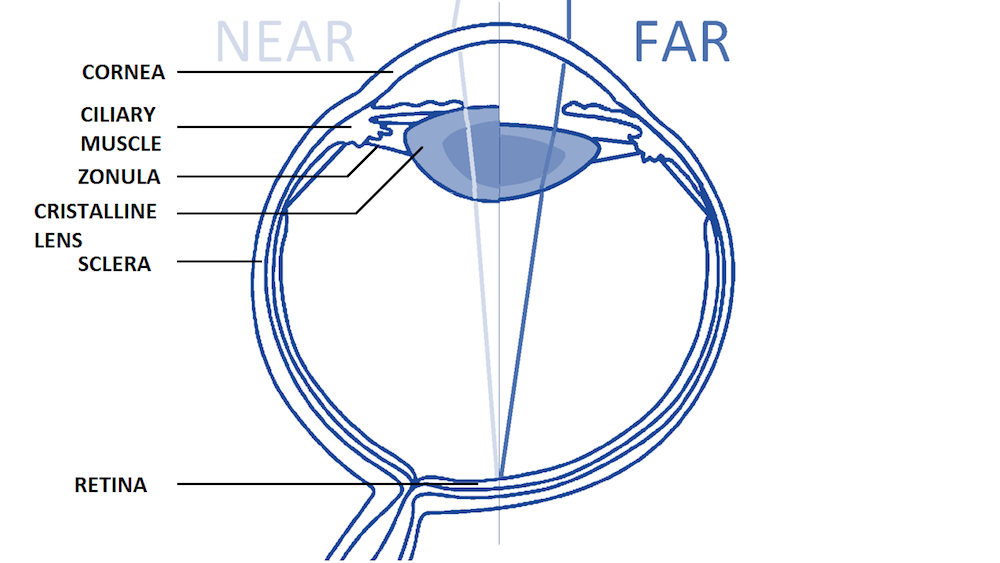
Anatomy of a human eye for the near and far vision, with the main structures involved in the accommodation process labeled. Image courtesy Kejako.
While corrective lenses, such as eyeglasses, are the safest and most reliable way to address vision problems associated with presbyopia, they do not address every problem associated with the presbyopia — and not everyone likes wearing spectacles.

Reading glasses have been around for quite a while to help correct visual impairment from disorders like presbyopia. This painting, called the “Glasses Apostle”, was painted by Conrad von Soest in 1403. Image in the public domain in the United States, via Wikimedia Commons.
Some people choose to undergo refractive surgery to address this type of near-vision loss. Currently, this surgery is invasive and can still come with visual compromises — patients may experience vision that produces a glare or halo or have problems seeing in dim lighting. Further, many in vivo imaging technologies available for these procedures are not able to accurately account for every factor or practical clinical measurement in the visual accommodation process.


Left: Halos at night. Right: Glare at night. Images courtesy Kejako.
To address these limitations as well as the root problem of presbyopia, David Enfrun, Aurélien Maurer, and Charles-Olivier Zuber at Kejako developed a 3D parametric mechanical model of the human eye as well as an optical evaluation technique using the COMSOL® software. According to Enfrun, cofounder and CEO of Kejako, the research team "decided to approach ophthalmology with an antiaging mindset," so they turned to simulation in order to look for a "biomechanical alternative to reading glasses and heavy surgeries." With their model, the team can use a reverse engineering technique to deduce nonmeasurable properties from in vivo imaging.
Modeling Solutions to the Age-Old Problem of Presbyopia
Because the visual accommodation process is so complex, simplifications are often made when it comes to modeling the eye and its components. For instance, many models are axisymmetric and do not account for the natural variability of the organs of the eye. The models focus on either the accommodation’s mechanical or optical aspects, meaning only a few of the eye components are modeled and material properties are approximated rather than taking real behaviors into account.
In vivo technologies for ophthalmology have contributed greatly to advances in 3D modeling, but each type has its pros and cons:
- Magnetic resonance imaging (MRI) provides the best results (low distortion, high resolution) for internal geometry but is hard to use outside of labs
- Optical coherence tomography (OCT) helps retrieve info on the optical axis but induces some spatial distortions
- Ultrasound biomicroscopy (UBM) gets images of nontransparent eye parts but induces high spatial distortions
After making corrections and extrapolating information from in vivo imaging, some material properties are still difficult to measure. What’s more, nonmeasurable properties are often essential when trying to correct presbyopia, such as the stiffness and the refractive index distribution in the crystalline lens.
Setting Up an Optomechanical Model of the Human Eye
In an effort to obtain this important data, the Kejako research team built a model of their own using the Nonlinear Structural Materials Module, Structural Mechanics Module, and Ray Optics Module; add-on products to the COMSOL Multiphysics® software.
First, they developed and validated a complete 3D nonaxisymmetric model of the human eye’s accommodation that includes the main organs involved in the visual accommodation process. Since the validated model proved capable of simulating presbyopia progression, the researchers were able to further develop the model geometries, including accounting for both nearsighted and farsighted geometries.
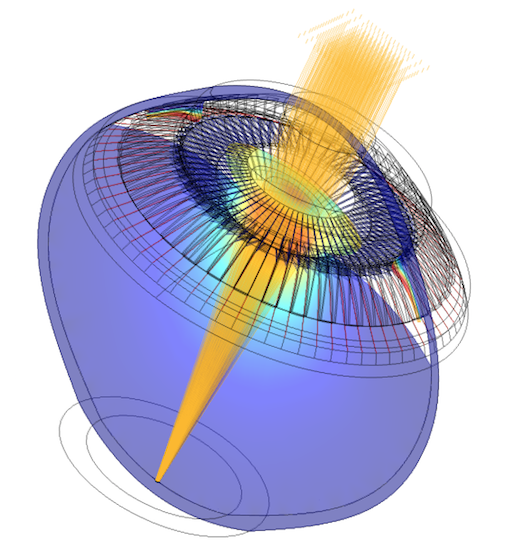
The parametric optomechanical model of the human eye developed by Kejako. Image courtesy Kejako.
The research team also used the CAD Import Module to prepare the model geometries based on an OCT scan of a relatively young eye belonging to a 22-year-old patient. While they used this imaging as a basis for their model, the researchers will eventually be able to help customize patient procedures by importing each patient’s biometry data into the model so they can “have an exact representation of each patient’s eye and its actual presbyopia stage.”
This could significantly advance presbyopia treatment, as according to Maurer, the current implant market is “like a ready-to-wear shop for shoes: a bunch of different sizes.” However, each person’s eye is different; the distances between components and their individual shapes creating a unique combination. In addition, Zuber says that not all patients at a given age are experiencing the same stage of presbyopia when it comes to lens hardening, and the lens properties are not “evenly distributed among patients.” Using simulation could help create optimized laser treatments that fit each person’s needs. As Maurer explains, “the combination of imaging, simulation, and laser enables us to make a patient-specific treatment.”
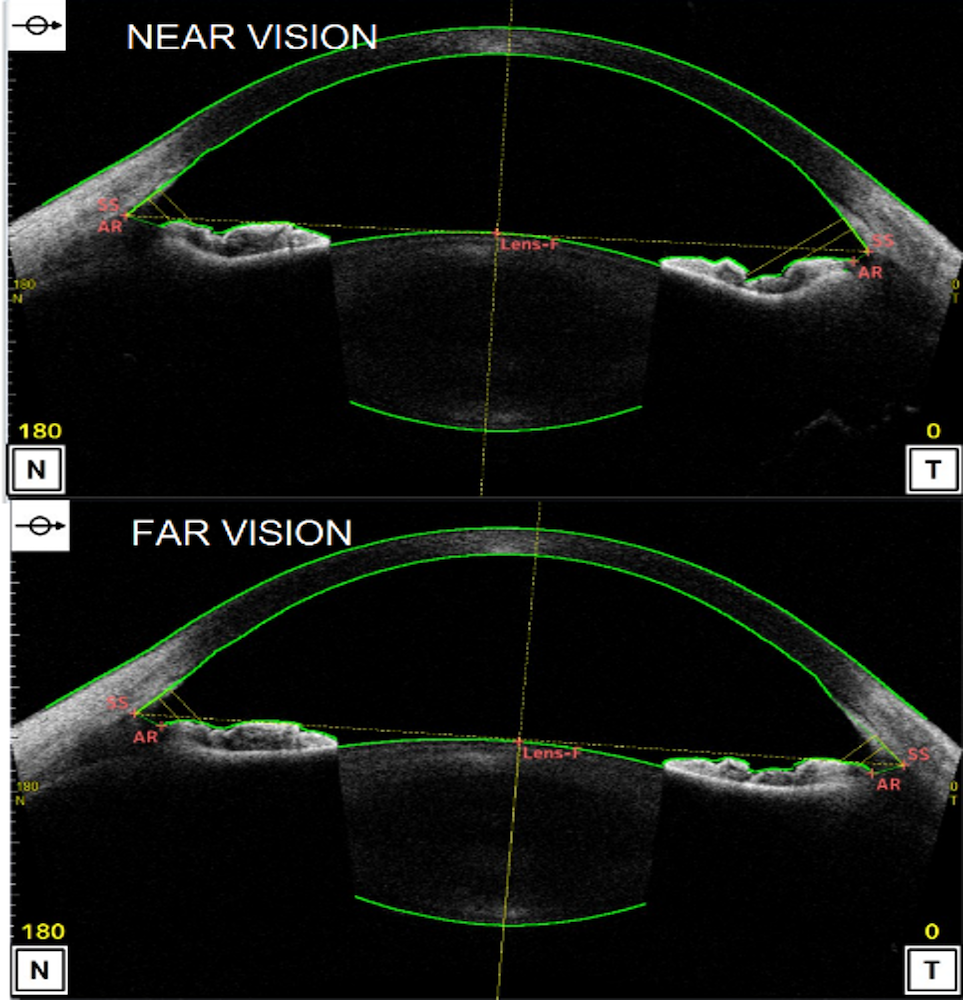
The OCT imaging provided the team with geometries in the optical axis for two optical stimuli: 0D for far vision and 6D for near vision. Measured in diopters, these geometries indicate the power of the lens and its ability to focus light on the retina. They used additional measurements and properties from validated experiments and reference data. The researchers were then able to submit the sample tissue to both mechanical and optical tests to increase their ability to obtain more material properties. The model was considered ready once the unaccommodated geometry entered a tolerance of +/-5% with the far vision measurement. (For more details, take a look at Kejako’s research paper, which was presented at the COMSOL Conference 2017 Rotterdam.)
OCT imaging of the subject (left) alongside a CAD simulation (right). Images courtesy Kejako.
Deducing the Refractive Index for 2 States of Vision
To model the refraction of the lens, the researchers used the Wall Distance interface to create a repartition of the refractive index that follows the deformation of the lens during accommodation. The team’s goal was to compute the refractive index and its spatial distribution for both farsighted vision and nearsighted vision conditions.
In their first study (“Test A”), they prepared the geometry to account for these extreme conditions, hypothesizing that the refractive index is homogeneous in the lens. They then applied a two-parameter function to the generated distance field to create a gradient of refractive index (GRIN) that lined up with natural optical properties.
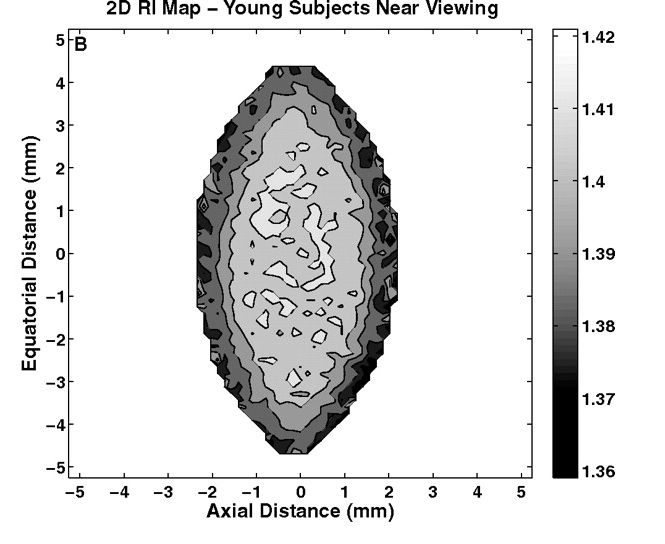
Left: A GRIN measured with MRI. Image from S. Kasthuriranagan et al., “In Vivo Study of Changes in Refractive Index Distribution in the Human Crystalline Lens with Age and Accommodation“, 2018. Right: Simulation showing 3D cuts of the distance gradient generated with the Wall Distance interface. Image courtesy Kejako.
The second study they prepared (“Test B”) focused on the model of the GRIN. By running parametric sweeps, the researchers sought to extract a unique couple of parameters for the GRIN that match both vision states.
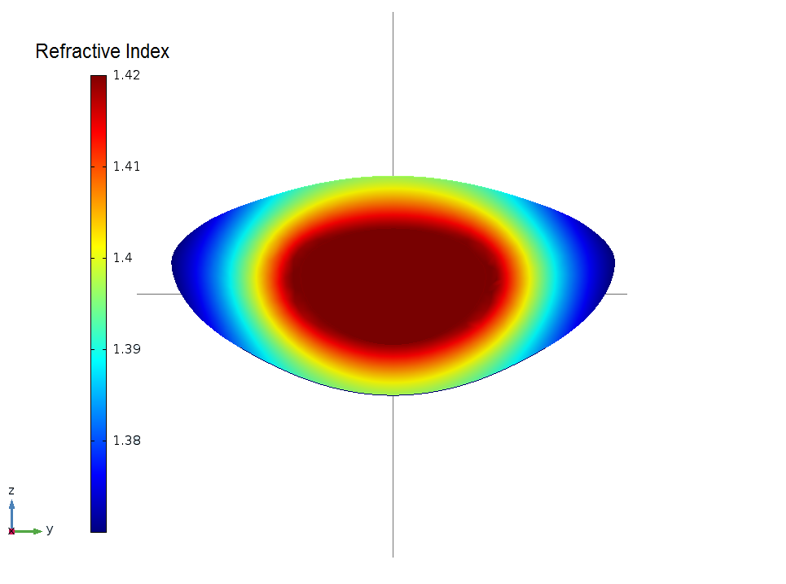
Map of a GRIN that matches the two states of vision. Image courtesy Kejako.
Evaluating the Simulation Results
After examining the overall simulation, the researchers were able to verify that their results for the 3D parametric human eye model geometry were consistent with scientific literature. For instance, the far-vision data has a less than 3% difference in the lens position and shape. In addition, the researchers found that the results for the individual studies are consistent with validated data. The values they obtained in Test A are well within the range of the equivalent measurements from verified studies, and the GRIN results in Test B are consistent for both visual conditions.
Based on these two studies, the team found some surprising results that helped inform their research and reverse engineering capabilities. For instance, contrary to their hypothesis that the refractive index is homogeneous in the lens, the results for Test A show that a unique homogeneous refractive index matching the amplitude of the patient’s stimuli (0 to 6D) could not be found. In addition, when the far-vision-matching homogeneous refractive index is used for near vision, it induces an accommodation amplitude of 4.35D instead of 6D — the homogeneous refractive index value needs to be much higher when computed for near vision.
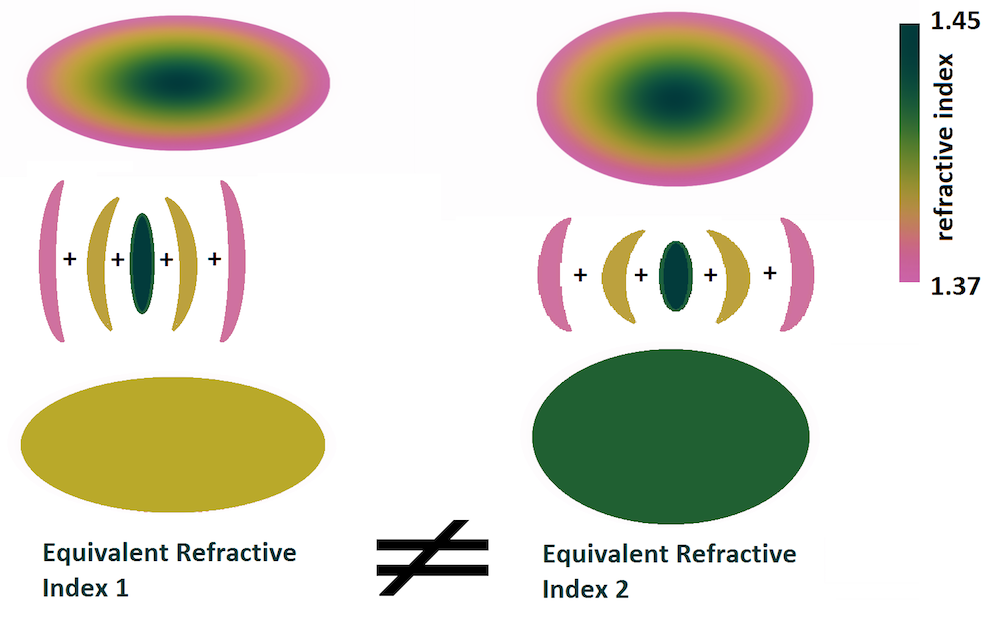
Based on their GRIN model results, the researchers also found something interesting concerning the natural optical structure: The human eye will induce a nonlinear response to try to maximize the optical power of the lens tissue. As shown below, to achieve the same maximal value of the plateau, the gradient induces bigger changes than the maximal values.
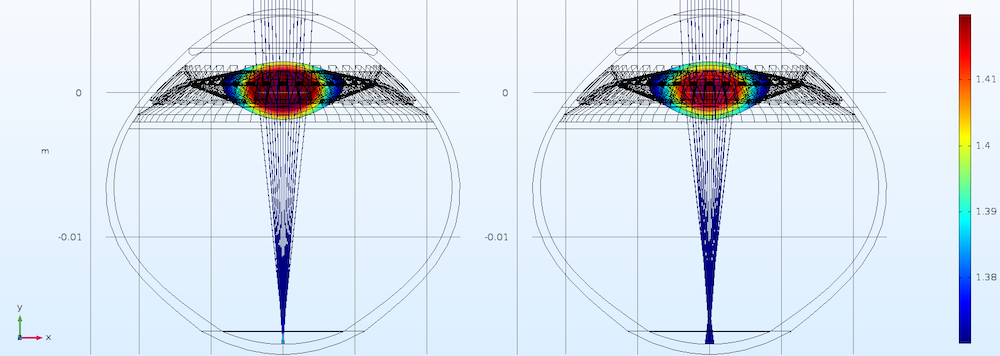
Effect of two different GRIN intensity parameters with the same plateau value in the far vision. Image courtesy Kejako.
Furthermore, due to the natural optical structure, the eye has a greater range of focus with a lower maximal value of the refractive index. Shown below is a schematic of the GRIN acting as a multiplicative factor for the accommodation. For each state of vision, the lens tissues move with the accommodation. The optical configuration for far vision is clearly quite different than the configuration for near vision. By inducing this nonlinear response, the GRIN contributes to improving the amplitude of vision.
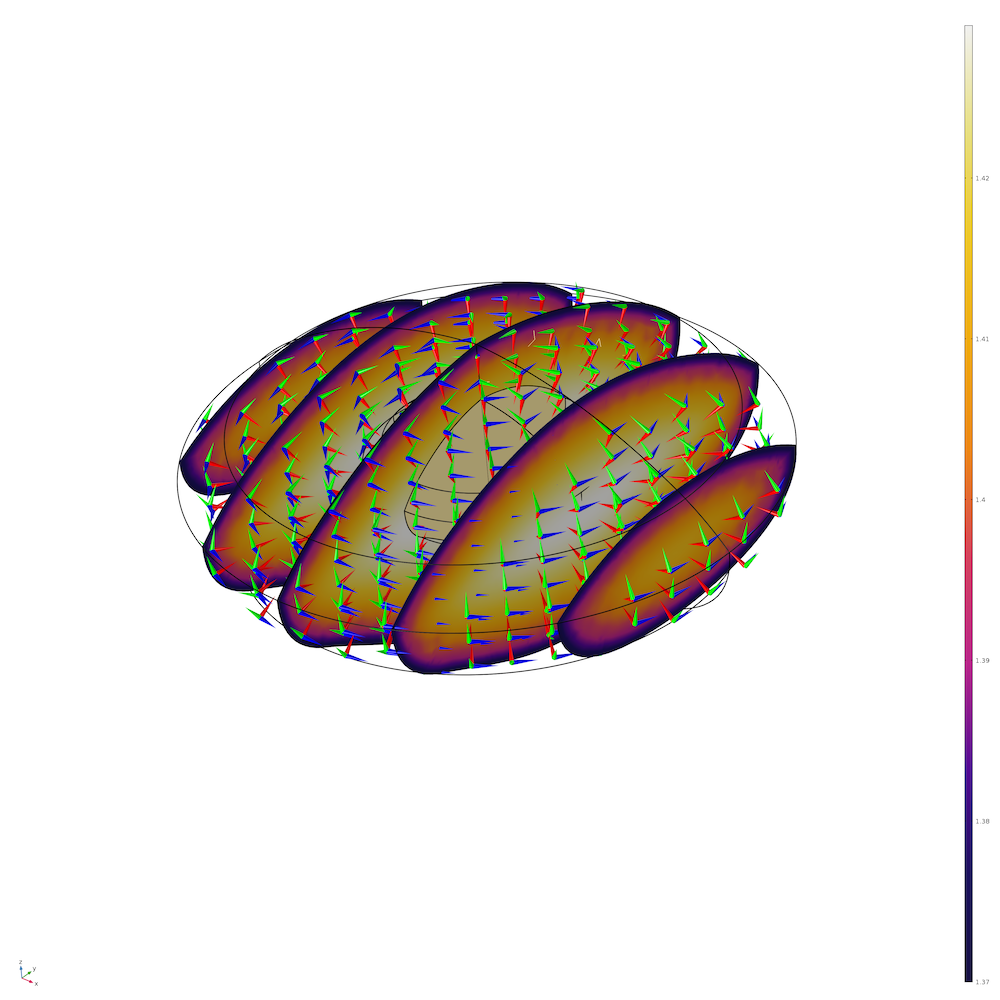
Finite multilayer representation of the GRIN with decomposition in equivalent lenses for each layer. Image courtesy Kejako.
Deducing nonmeasurable properties like the ones above could lead to important developments in eye care, such as the prevention and correction of presbyopia. The Kejako researchers quickly understood the value of this ability in the ophthalmology field. After developing and validating their model, they opened an internal department dedicated to answering research and development questions that their tools and simulations can help answer.
The Future of Simulation in Eye Care
In the future, simulation could help the team learn more information, such as what effect laser treatment has on a patient’s amplitude of accommodation. The reverse engineering technique could also come into play in their plans to determine the mechanical properties of a lens from elastography imaging.
Already, their model results have helped answer some questions about visual accommodation. Soon, the researchers hope their model will not be limited to visual accommodation and can be used in diagnostics and the optimization of personalized medical procedures as well. To accomplish this, the team is working on improving the eye model so that they can simulate potential solutions for treating presbyopia.
Enfrun explains that they’re further developing the model for lab testing by “increasing the physical interpretation of what can happen in lab testing,” whether ex or in vivo (currently, the researchers are testing ex vivo feasibility). With improvements like this, the model could reduce the number of biological (e.g., in vivo) tests needed, which was one of the team’s goals. Enfrun says they chose simulation “as a tool for us to understand the visual accommodation process without further ex vivo/in vivo testings.”
For more information about the 3D full-eye model, you can read the research paper by clicking the button below:
Learn even more about Kejako’s optomechanical modeling research on pages 6–9 of Multiphysics Simulation 2018.





Comments (0)