Studies and Solvers Updates
Support for NVIDIA® GPUs
GPU support has been added for pressure acoustics and surrogate model training. This functionality is available for systems equipped with a compatible NVIDIA® GPU.
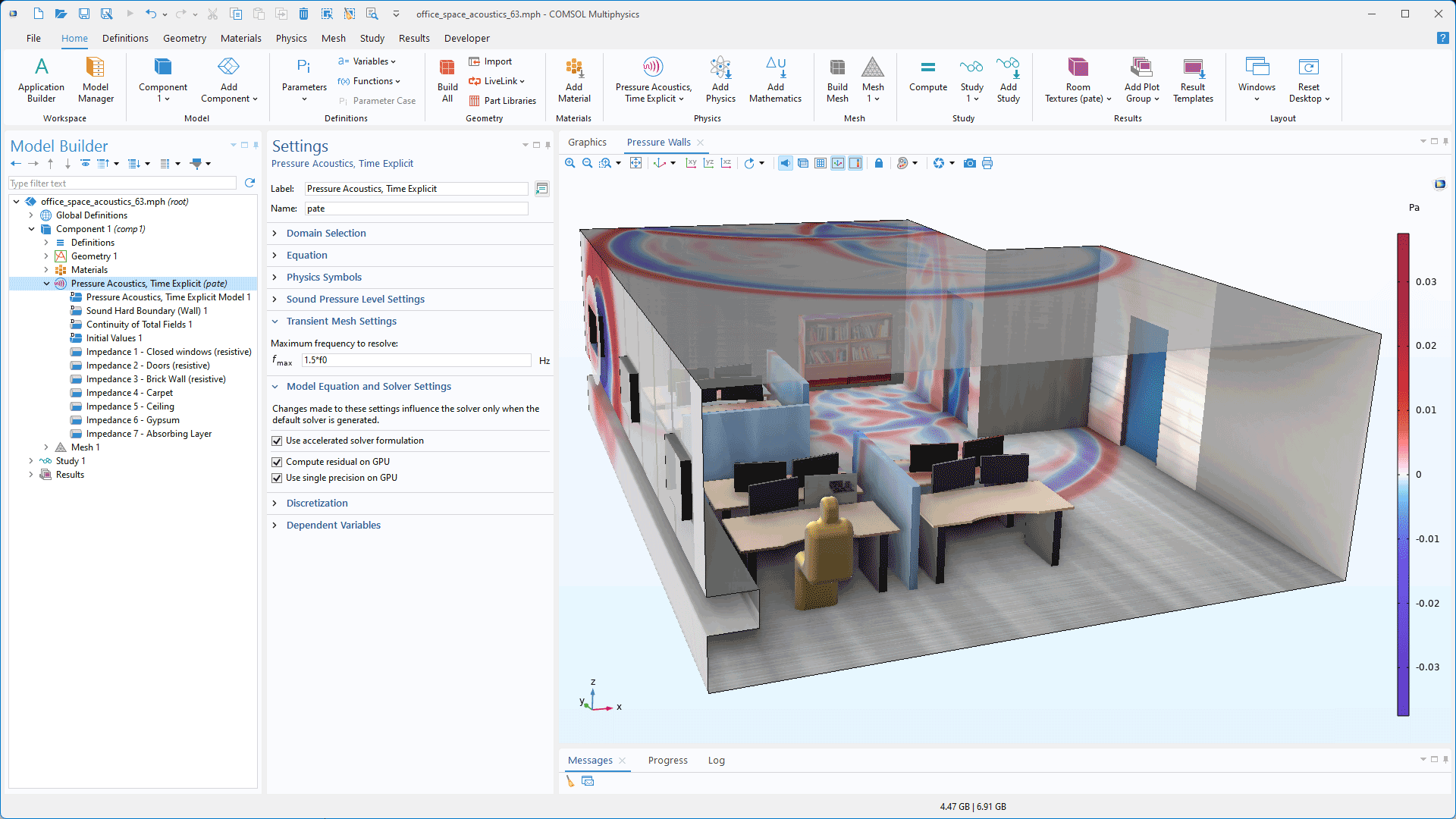
GPU Acceleration for Time-Explicit Pressure Acoustics
Linear time-explicit pressure acoustics models can now be solved using an accelerated formulation that supports realistic impedance boundary conditions. This acceleration can be significant increased when the formulation is used with an NVIDIA® GPU card, though performance gain depends on the hardware. To enable this functionality, a CUDA® Toolkit must be installed. (The toolkit's path can be specified during installation.) This functionality can be seen in the Acoustics of an Open-Plan Office Space tutorial model. For more details, see the Acoustics Module release highlights.
GPU Acceleration for DNN Surrogate Model Training
GPU support for training DNN surrogate models has been added, significantly speeding up the training process and enabling faster development of surrogate models for use in apps and various simulation contexts. To activate this functionality, ensure that the CUDA DNN Support option is selected on the Products page of the COMSOL Installer. Additionally, the NVIDIA® CUDA® Toolkit must be installed, which can be downloaded from the NVIDIA® website.
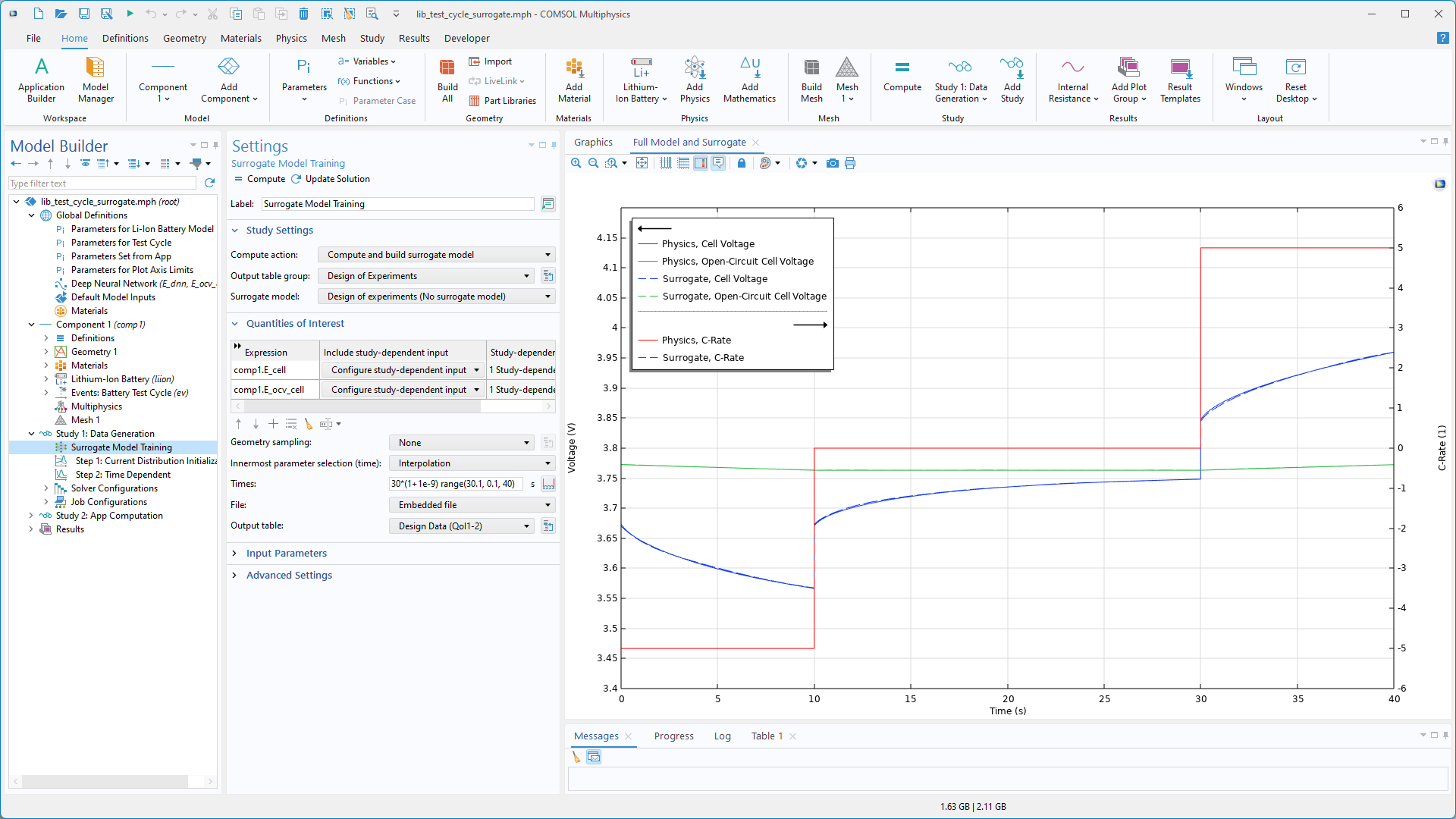
Improvements for Surrogate Model Data Generation
Generating space-, time-, and frequency-dependent data for use in DNN surrogate models is now significantly easier.
A Geometry Sampling option is available under the new Surrogate Model Sampling submenu within the Definitions for model components. This feature enables data sampling directly in domains, at boundaries, along edges, or at vertices, eliminating the need for file export or import workflows.
Additionally, a new Study-dependent input option in the Surrogate Model Training study enables the inclusion of time-dependent or frequency sweep results in the training data. This simplifies the incorporation of dynamic or frequency-dependent data into surrogate models.
Optimization
Discrete Adjoint Solver Type
A new Time discrete adjoint solver type is available for optimal control and time-dependent parameter estimation. This solver type is based on a discrete sensitivity method, which provides enhanced robustness, improved accuracy, and faster performance for gradient-based optimization with the Time-Dependent Solver.
In transient parameter estimation problems, significant speed improvements are achieved with the sparse nonlinear optimizer (SNOPT) or interior point optimizer (IPOPT) solvers. This is due to the aggregated sensitivity of the entire objective being computed in a single pass instead of separate calculations for each measurement point. The previous continuous sensitivity method is still available, but it is no longer the default for transient optimization.
Both the discrete and continuous methods reduce memory consumption through checkpointing, which involves recomputation of the forward solution. In addition, there is a new Out-of-core option that can alternatively be used for forward solution handling, which instead uses temporary disk space to avoid recomputation.
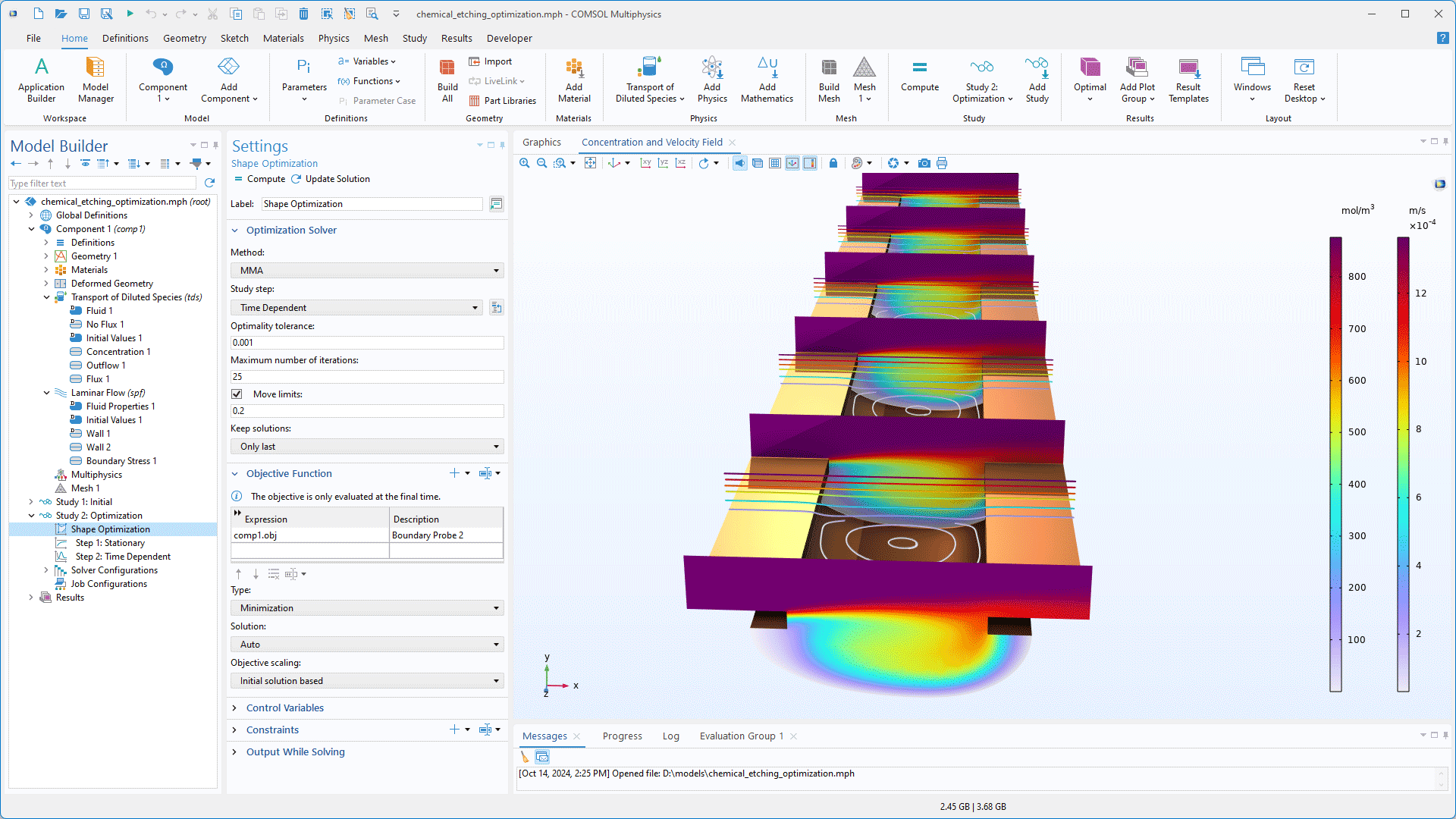
Efficient Global Optimization
A new gradient-free optimization solver that uses the efficient global optimization (EGO) algorithm has been introduced. This solver is well suited for tackling optimization problems with several local optima, as it does not require an initial guess for the control parameters and is less prone to getting trapped at a local minimum — making it especially useful for challenging optimization problems, such as those encountered in frequency-domain analyses.
While the EGO solver is slower than local optimization methods due to its global search strategy, it provides valuable robustness in navigating complex solution landscapes. After running the EGO solver, it is recommended to further process the results using a local optimization method to refine the solution. Additionally, the solver enables the inspection of the underlying surrogate model used for the analysis, providing further insight into the optimization process.
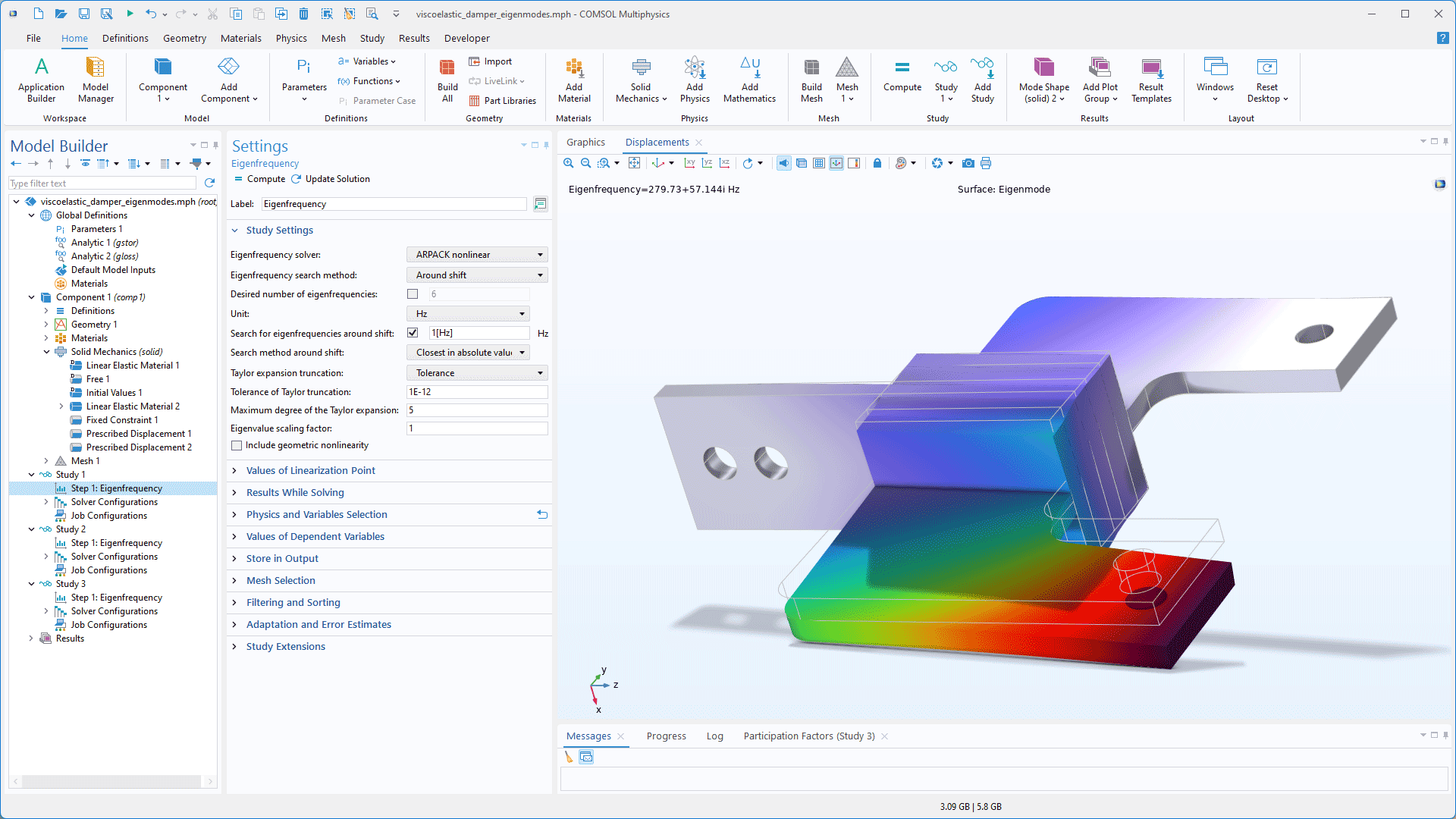
Nonlinear Eigenvalue Solver and Improved Sorting
A new nonlinear eigenvalue solver based on the ARPACK library is now available as an option within the eigenvalue solver, eliminating the need for manual iterations when solving for nonlinear eigenvalues. This is useful for structural analysis with viscoelastic materials, electromagnetic mode analysis, and more.
Additionally, a new Filtering and Sorting section has been added to the settings of the Eigenvalue, Eigenfrequency, and Boundary Mode Analysis study steps. This makes it possible to apply filter expressions, such as real(freq) + 1e-6 > 0, and sort eigensolutions by various criteria, such as real or imaginary parts, their magnitudes, or absolute values, in ascending or descending order. Sorting options are also available in the Eigenvalue Solver and Combine Solutions feature nodes when working with eigenvalue-type solutions.
Proper Orthogonal Decomposition (POD) Reduced-Order Model
A new model reduction technique, POD, has been added. The main idea of POD is to use snapshots of a model to perform a decomposition of a physical field using ideas from principal component analysis. POD can be useful for problems that are parameterized in the frequency domain.
Solver Improvements
Adaptive Tolerance for Linear Solvers
When solving nonlinear problems, it is now possible to enable the tolerance in the linear solver to vary adaptively. This can lead to substantial speedups. This method uses error estimation from the nonlinear solver to solve with lower accuracy when far from the solution and higher accuracy when approaching convergence. Adaptive tolerance in the linear solver is supported for the Constant damping method. It is also supported together with the pseudo-time-stepping method popular for stationary CFD problems.
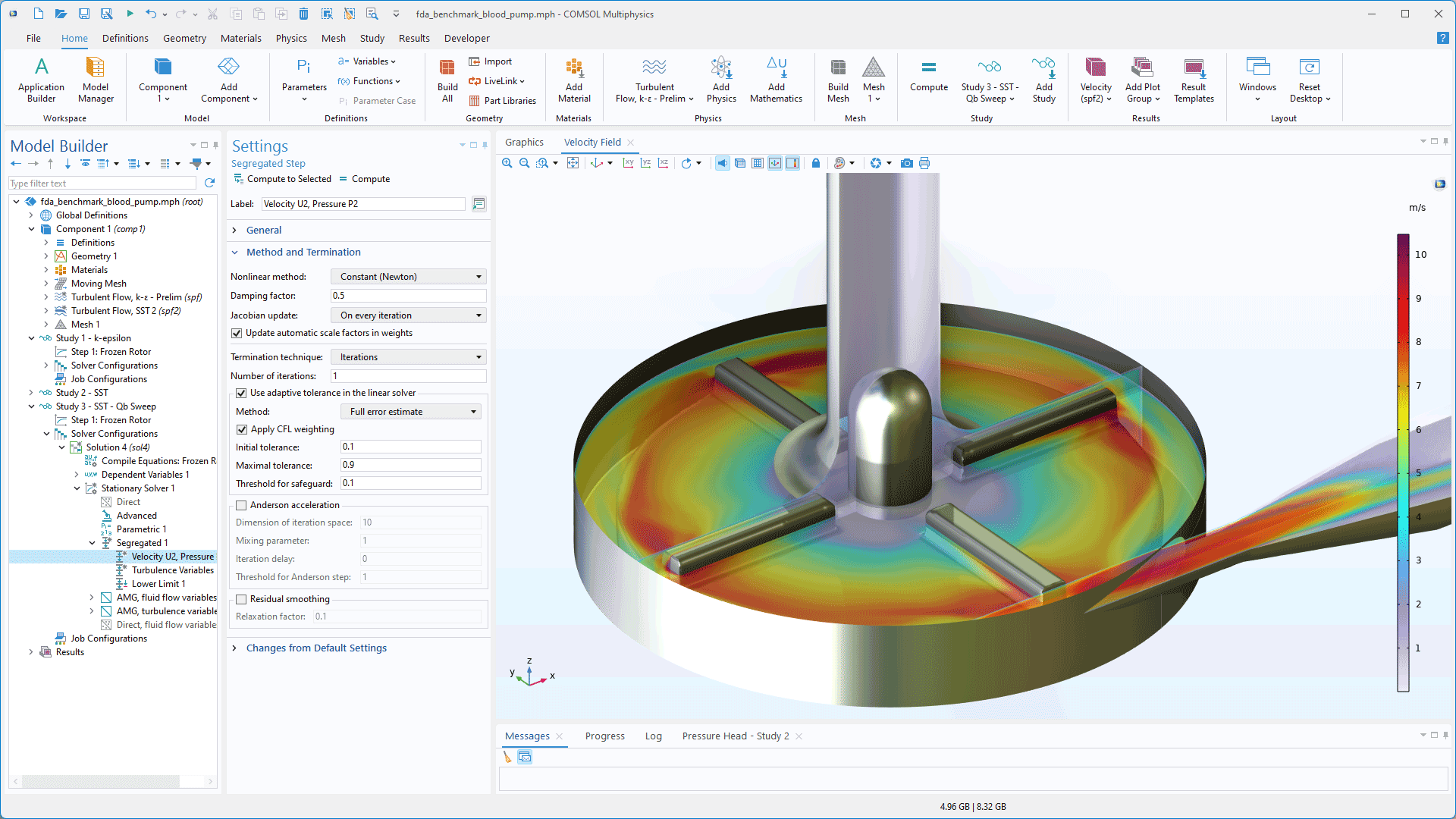
Scaling for the Algebraic Multigrid (AMG) Method
Row scaling for the AMG method can now be determined automatically. Enabling Row equilibration under the Advanced node of the Stationary Solver node will result in the automatic selection of an appropriate scale for the multigrid solver.
Faster Default Solvers for Stationary Fluid Flow
New default solver settings for stationary fluid flow simulations provide substantial solution-time reductions in a majority of cases. The new settings are applied to the solver sequence when a Stationary study or Stationary study step is added, when the solver configurations are reset to their defaults, and to existing stationary studies for which the Solver Configurations node has not been edited.
